Starting Out
Atari Animation
Lesson 5: Introducing Bit-Mapping
by Robin Alan ShererThis series for intermediate BASIC programmers explains bow to make Atari graphics move. But any 8-bit Atari user with minimum 32K memory disk or cassette, can enjoy the short BASIC type-in graphics demonstrations accompanying each lesson.
Everything you see onscreen, whether text or graphics, is represented at the lowest level by bits which turn on or off. Each memory location in RAM can hold a number from 0 to 255. These numbers are stored by bits numbered 0 to 7 in each memory location. To create text and graphics onscreen, the computer's designers built programs into the computer telling it how to interpret those bits.
GRAPHICS 8
Graphics 8 is easier to understand than other graphic modes. The screen is divided into a grid of 320 dots across and 192 dots down. Each dot can be turned on or off. In Graphics 8, each bit in screen memory represents a dot. Turn a bit on or off, and the corresponding dot responds exactly the same way.Because each byte has eight bits and each line is 320 dots across, it follows that each Graphics 8 line contains 40 bytes. That's a total of 7,680 bytes of screen memory (40 x 192).
Since one byte holds eight dots instead of one, turning individual bits on and off can be frustrating (especially from BASIC). Another complication is color. You have a choice of two—on or off, 0 or 1, blue or white, background or foreground.
Giving a bit a value of 1 turns it on, and 0 turns it off. White is the foreground color—in which the letters are drawn in BASIC—and blue is the background color.
In BASIC, if we forget to set colors, then the machine uses built-in defaults—in this case, blue for background and white for foreground. To change these colors, either use the SETCOLOR command or POKE colors directly into the memory locations that hold the color information. Rarely will you want to change all of this directly. It's much easier to PLOT and DRAWTO.
GRAHPICS MODE SUMMARIES
DISPLAY TYPE
SCREEN SIZE (COLUMNSxROWS)
MEMORY USED (BYTES)
DEFAULT COLORS
SET COLORS (N)
POKE ADDRESS
COLOR (N)
TWO SHADES OF ONE COLOR
GRAPHICS 8
320x160 SPLIT
320x192 FULL8112 SPLIT
8238 FULLLIGHT BLUE
DARK BLUE
BLACK1
709
1
2
710
0
4
712
BORDER
TWO COLORS
GRAPHICS 4
80x40 SPLIT
80x48 FULLMODE 4
694 SPLIT
696 FULLORANGE
BLACK0
4708
7121
0
GRAPHICS 6
160x80 SPLIT
160x96 FULLMODE 6
2174 SPLIT
2184 FULL
FOUR COLORS
GRAPHICS 3
40x20 SPLIT
40x24 FULL434 SPLIT
432 FULLORANGE
LIGHT GREEN
BLUE
BLACK0
1
2
4708
709
710
7121
2
3
0
GRAPHICS 5
80x40 SPLIT
80x48 FULL1174 SPLIT
1176 FULL
GRAPHICS 7
160x80 SPLIT
160x96 FULL4190 SPLIT
4200 FULL
GRAPHICS 4 AND 6
 As in Graphics 8, the dots in Graphics 4 and 6 can be either on or off. The difference is the larger sizes of dots in GR. 4 and 6. Screen memory in these modes works the same way as in GR. 8, but there can be fewer of those big GR. 4 and 6 dots onscreen. Thus less screen memory is needed, which gives you more room for your program and data.
As in Graphics 8, the dots in Graphics 4 and 6 can be either on or off. The difference is the larger sizes of dots in GR. 4 and 6. Screen memory in these modes works the same way as in GR. 8, but there can be fewer of those big GR. 4 and 6 dots onscreen. Thus less screen memory is needed, which gives you more room for your program and data.
GRAPHICS 3,5 AND 7
In these Graphics modes, not only can the pixels be on, but they each can have one of three colors-meaning four possibilities per pixel, not just two. But the catch is that we use two bits per pixel instead of one. So in the four-color modes, each byte of screen memory holds four dots instead of eight. Here's how they can be arranged:
| BIT PATTERN | USES COLOR |
| 00 | 0 |
| 01 | 1 |
| 10 | 2 |
| 11 | 3 |
These two bits tell your Atari chip which color to give a particular dot, but how does it know what the four colors are? After all, the Atari has 256 of them to choose from. As in Graphics 1 and 2, we use the four color registers. The difference, however, is that the bit combinations don't refer to the same color registers as they did for the characters.
| BITS | REGISTER | LOCATION |
| 00 | background | 712 |
| 01 | 0 | 708 |
| 02 | 1 | 709 |
| 03 | 2 | 710 |
BIT MAPPING
Now we are ready to explore what can be done with bitmapped graphics modes.You have seen that computer graphics is essentially getting bits turned on and off in the right places. Depending on the graphics mode you choose, these bits will be "translated" to the screen as pixels of varying sizes and color.
The only practical use for straight BASIC in drawing and PLOTting is to create backgrounds. We want to create shapes and make them flow gracefully enough to appear lifelike. We can either move our background—a city, mountains, etc.—or our players—cars, spaceships, people, etc. But you can animate any of these faster and more powerfully from BASIC with machine language subroutines.
Another approach to animation uses the PLOT command. To get the effect of movement with this method, you must PLOT a point, erase it, PLOT it again one place over, erase it and so on. The following program draws an orange dot that you can move with the joystick.
1000 REM ATARI ANIMATION, LESSON 5, DOT.BAS, PART 1
In this first example program, the dot leaves a trail—we're not so much animating as drawing. To get the desired effect, we must erase the trail by plotting the exact same shape using the background color in the same position once occupied by the orange dot. Below is a different method. Type it in as an addition to the previous lines.
1010 REM BY ROBIN SHERER
1020 REM (c)1987. ANTIC PUBLISHING ...
...
1030 GRAPHICS 4:POKE 764,255
1040 V=STICK(0)
1050 SETCOLOR 2,0,0:COLOR 2
1060 Y=Y+(V=13)+(V=9)+(V=5)-(V=10)-(V=14)-(V=6)
1070 X=X-(V=10)-(V=11)-(V=9)+(V=6)+(V=7)+(V=5)
1080 IF X<1 THEN X=1
1090 IF X>79 THEN X=79
1100 IF Y<1 THEN Y=1
1110 IF Y>39 THEN Y=39
1120 COLOR 1:PLOT X,Y:IF PEEK(764)=255 THEN 1040
10 REM ATARI ANIMATION, DOT, PART 2
The difference between the two dot routines is subtle, but important. It lies in the way the programs use the X and Y variables.
1060 IF V=14 THEN Y=Y-1:PLOT X,Y+1
1065 IF V=13 THEN Y=Y+1:PLOT X,Y-1
1070 IF V=11 THEN X=X-1:PLOT X+1,Y
1075 IF V=7 THEN X=X+1:PLOT X-1,Y
In the first example, X and Y contain the current position of the dot. In the second example, X and Y contain the previous position of the dot. And if we know the previous position of the dot, we can erase its trail.
Also, you can only move the joystick horizontally or vertically. To move it diagonally, you'd need several more program lines.
PLOTting can be tedious, especially if you have a lot of points to plot. Here's an example:
5 REM ATARI ANIMATION, LESSON 5, BITMAN.BAS
Even this takes a while to draw. Fortunately we already saw that using character sets was much quicker and gave an almost cartoon-like quality to the shape. But bitmapped Graphics modes can be used for nice backgrounds.
10 REM BY ROBIN SHERER
15 REM (c)1987, ANTIC PUBLISHING
20 GRAPHICS 5+16
30 COLOR 1:RESTORE 60
40 READ X,Y:IF X=0 THEN 102
50 PLOT X,Y:GOTO 40
60 DATA 9,23,10,23,11,23,9,24,10,24,11,24,10,25,8,26,9,26,10,26,11,26,12,26,7,27,9,27,10,27,11,27,13,27
70 DATA 6,28,9,28,10,28,11,28,14,28,9,29,10,29,11,29,9,30,10,30,11,30,9,31,11,31,8,32,12,32,7,33,13,33,7,34,13,34
80 DATA 7,35,8,35,9,35,13,35,14,35,15,35,0,0,0
102 COLOR 0:RE5TORE 60
103 READ X,Y:IF X=0 THEN 120
104 PLOT X,Y:GOTO 103
120 REM
150 COLOR 1:RESTORE 190
170 READ X,Y:IF X=0 THEN 211
180 PLOT X,Y:GOTO 170
190 DATA 9,23,10,23,11,23,9,24,11,24,10,25,8,26,9,26,10,26,11,26,12,26,7,27,9,27,10,27,11,27,13,27
200 DATA 7,28,9,28,10,28,11,28,13,28,9,29,10,29,11,29,9,30,10,30,11,30,9,31,11,31,9,32,11,32,8,33,12,33
210 DATA 8,34,12,34,8,35,9,35,10,35,12,35,13,35,14,35,0,0
211 COLOR 0:RESTORE 190
212 READ X,Y:IF X=0 THEN 230
213 PLOT X,Y:GOTO 212
230 REM
270 COLOR 1:RESTORE 300
280 READ X,Y:IF X=0 THEN 321
290 PLOT X,Y:GOTO 280
300 DATA 9,23,10,23,11,23,9,24,11,24,10,25,8,26,9,26,10,26,11,26,12,26,7,27,9,27,10,27,11,27,13,27
310 DATA 6,28,9,28,10,28,11,28,14,28,9,29,10,29,11,29,9,30,10,30,11,30,9,31,11,31,8,32,12,32
320 DATA 7,33,13,33,7,34,13,34,7,35,8,35,9,35,13,35,14,35,15,35,0,0,0
321 COLOR 0:RESTORE 300
322 READ X,Y:IF X=0 THEN 340
323 PLOT X,Y:GOTO 322
340 REM
380 COLOR 1:RESTORE 410
390 READ X,Y:IF X=0 THEN 432
400 PLOT X,Y:GOTO 390
410 DATA 9,23,10,23,11,23,9,24,10,24,11,24,10,25,8,26,9,26,10,26,11,26,12,26,7,27,9,27,10,27,11,27,13,27
420 DATA 7,28,9,28,10,28,11,28,13,28,9,29,10,29,11,29,9,30,10,30,11,30,9,31,11,31,9,32,11,32,8,33,12,33
430 DATA 8,34,12,34,8,35,9,35,10,35,12,35,13,35,14,35,0,0
432 COLOR 0:RESTORE 410
433 READ X,Y:IF X=0 THEN 450
434 PLOT X,Y:GOTO 433
450 REM
460 GOTO 30
BIT-MAPPED MODES
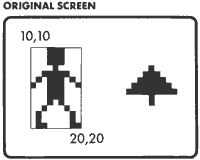 The best way to use a graphics mode in a program is to use a graphics editor to draw the entire screen, then SAVE it to disk. When your program needs that screen, you can bring up the data quickly and place it right into the correct memory area for screen data.
The best way to use a graphics mode in a program is to use a graphics editor to draw the entire screen, then SAVE it to disk. When your program needs that screen, you can bring up the data quickly and place it right into the correct memory area for screen data.The idea of moving characters around the screen isn't much different from cutting and pasting paper shapes. First you must define a set of dots, then instruct the computer with a machine language routine to move all dots between, for example, screen coordinates 10,10 and 20,20.
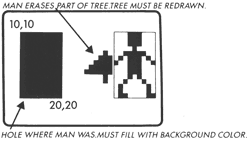 Great, but what if the "box" we placed our picture in had part of another shape in it? Then you must tell the computer, via another machine language routine, to put those dots at a different location. The only practical way to cut out a shape is with a box that surrounds it. Fill any holes with background color.
Great, but what if the "box" we placed our picture in had part of another shape in it? Then you must tell the computer, via another machine language routine, to put those dots at a different location. The only practical way to cut out a shape is with a box that surrounds it. Fill any holes with background color.
The disadvantages of animating with memory move routines are subtle. If part of your picture resides outside the area you have moved, that portion will stay put. Also, the area that is moved will overwrite everything in the area where it's placed.
The only solution would be to write a complicated machine language routine to store the picture we're cutting out before the shape messes it up, then restore it after the shape moves across the background. Since this must be done for each pixel in the "box," it can be very complicated.
However, the best way to animate small shapes is with Player/Missile graphics—which will be introduced in later lessons.
GRAPHICS MODE TEXT
Adding text to Graphics modes is handy for everything from game scores to business chart labels. The following examples look at the character set in RAM, take apart the bits for the desired letters, and "paint" them onto your graphics screen.
2 REM M8TXT.BAS
Line 20 contains the string you want to plot, and the X,Y position to place it in. Remember to use the same limits as the Graphics modes you're in.
4 REM BY ROBIN SHERER
6 REM (c)1987, ANTIC PUBLISHING
10 DIM TEXT$(4),HOLD$(1)
20 TEXT$="TEST":X=5:Y=20:REM (CHANGE T0 Y=10 FOR GR.4)
30 GRAPHICS 8+16:SAVMSC=PEEK(88)+PEEK(89)*256:WIDTH=40
40 POKE 710,0
50 SCRN=SAVMSC+Y*WIDTH+X
60 FOR Z=1 TO LEN(TEXT$)
70 HOLD$=TEXT$(Z,Z):GOSUB 140
80 CHAR=PEEK(756)*256+TEMP*8
90 FOR ROW=0 TO 7
100 POKE SCRN+ROW*WIDTH,PEEK(CHAR+ROW)
110 NEXT ROW:SCRN=SCRN+1:NEXT Z
120 COLOR 1:PLOT 10,10:DRAWTO 40,40
130 GOTO 130
140 TEMP=ASC(HOLD$):IF TEMP>127 THEN TEMP=TEMP-128
150 IF TEMP>31 AND TEMP<96 THEN TEMP=TEMP-32:RETURN
160 IF TEMP<32 THEN TEMP=TEMP+64
170 RETURN
Line 30 finds the start of screen memory and places this address into SAVMSC.
Line 40 sets the background color.
Line 50 calculates where to start placing data in the screen memory.
Lines 60-70 and the useful subroutine at 140-170 break down the characters to their position internally in the Atari's ROM character set. If internal codes matched ASCII codes, this wouldn't be needed.
Line 80 checks the Character Base Register (location 756, $02F4) to find the start of the character set. This routine will work with your own redefined character sets, too. (See Lesson 3, Antic, Aug. '87, for more information on redefined character sets.)
Lines 90-110 break down the eight horizontal "layers" of the character and POKE it directly into memory.
Line 120 plots a line to show you we aren't faking anything. Your screen really has letters and graphics overlapped.
To change the routine for Graphics 4 or 6, change the Graphics mode number (line 30) from 8 to 6 (or 4). Then, change NUMCOL (line 30) from 40 to 20 (for Graphics 6) or 10 (for Graphics 4). If you're using Graphics 4, you'll also have to change the instruction Y=20 to Y=10 in line 20.
FLAPPING BIRD
This month's demonstration listing combines the short routines from the article. It draws a flapping bird which you can control with your joystick. It is a very simple, bare-bones example that you'll find easy to understand and modify.Type in Listing 1, VBIRD.BAS, checking it with TYPO II, and SAVE a copy to disk before you RUN it. When RUN, VBIRD draws a simple mountain scene in Graphics 8. Then, the listing uses routines from M8TXT.BAS to successively plot the "v", "^" and " " characters, giving the illusion of a flapping bird. We've also borrowed the animation routines from the DOT routines to allow you to move the flapping bird up and down.
RECOMMENDED BOOKS
Your Atari Computer by Lon Poole. Osborne/McGraw-Hill, 2600 Tenth Street, Berkeley, CA 94710. (415) 548-2805. $17.95, 474 pages.Mapping the Atari by Ian Chadwick. Compute! Publications, Inc. (ABC), 825 Seventh Avenue, New York, NY 10019. (212) 887-5928. $16.95, 272 pages.
Robin Sherer co-wrote four Atari programming books. He presently programs for Boeing in Seattle.
Listing 1 VBIRD.BAS Download