EQUIVALENCE
New way to speed up your BASIC programs.
Equivalence teaches intermediate-level programmers how to use a powerful technique that speeds up common BASIC operations by as much as 150 percent. Included BASIC demonstration programs work on all 8-bit Atari computers of any memory size, with disk drive. The article also explains how to use the Turbo BASIC XL language for even greater speed.
Atari BASIC is a very friendly programming language, but certain operations can be rather slow. Disk I/O, integer calculations, FOR-NEXT loops, etc. all involve floating-point calculations requiring six storage bytes for each variable used. These operations are slow because they require many integer-to-floating-point and floating- point-to-integer conversions.
String operations, on the other hand, are quite speedy. "Equivalencing" lets you apply these speedy operations to other types of data. Equivalencing can make numeric disk I/O and other operations run up to 150 times faster.
EQUIVALENCING
Equivalencing simultaneously treats blocks of data as string data and as floating-point data.
Your Atari stores strings and numbers as bytes in RAM. BASIC uses a series of tables to remember which of these bytes are part of strings and which bytes represent floating-point numbers. By changing these tables you can take a series of bytes that represent a floating-point number and make BASIC treat these bytes as a string as well as a number.
These tables also contain the locations of all the variables in your program. They work like an address book. Once BASIC determines whether a series of bytes contain a string or a floating-point number, it goes back to these tables to find the location of these bytes.
Change these tables and you change the memory locations that BASIC will search for the values of your variables. It's like telling your mother-in-law that you moved to Borneo. The next letter she sends you will end up in Indonesia.
By altering the values in these tables, you can take any block of memory and treat it like a string.
Equivalencing techniques let you take advantage of BASIC's speedy string operations while avoiding time consuming floating-point conversions.
SPEED DEMOS
Listing 1 uses sound to illustrate this dramatic improvement in speed. Type in Listing 1, EQUIV1.BAS, check it with TYPO II and SAVE a copy to disk. Be sure to remove the TYPO II program, as described in the TYPO II instructions, before you RUN the program. The first part of the program plays all four voices using BASIC's SOUND command.
This part of the program can be slightly accelerated by POKEing the sound data directly into the audio control registers (memory locations 53760-53768).
The second part of the program uses an equivalenced string to fill all audio control registers at once. First, the program DIMensions a string called S$. Then it alters the variable tables, fooling BASIC into thinking that S$ has moved to a different address (the audio control registers).
The next time BASIC looks for the bytes in S$, it'll end up at the audio control registers. Since BASIC thinks that S$ is located at the audio control registers, anything we put into S$ will appear in these registers.
Here's an example. If we tell BASIC that S$ begins at memory location 53760 (the address of the first audio control register) then:
S$(1)= "A"
ASC("A")=65
has the same effect as (but much quicker than):
POKE 53760,65
We've just equivalenced a string variable to a specified block of memory--the audio control registers. Listing 2 shows you how to equivalence a string to a numeric array to speed up data handling.
DATA HANDLING
Listing 2 creates a sample floating- point array, M(), writes it to disk and reads it back again. The first time the program does this, it uses GET, PUT and other conventional methods of handling data. Then, the program does the same thing all over again, but this time it uses speedy equivalencing techniques.
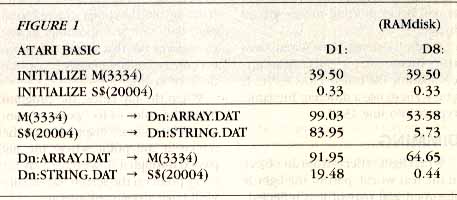
The entries in figure 1 are the run times in seconds for each part of Listing 2 when M() has 3,334 elements.
Type in Listing 2, EQUIV2.BAS, check it with TYPO II and SAVE a copy to disk. Be sure to remove the TYPO II program, as described in the TYPO II instructions, before you RUN the program.
When RUN, the program asks you to choose the size of the sample floating-point array. As written, the program cannot handle such arrays DIMensioned above 4,000.
Next, the program equivalences array M() to a string, S$, and begins filling M() with numbers. Since M() and S$ are equivalenced, every value placed in M() also appears in S$, but in a slightly different form.
Since BASIC stores numbers as six-byte binary coded decimals (BCD), your equivalenced string requires 6 characters for each floating-point number. For example, the number 41.4243444 is is internally represented as @ABCDE.
So if you wanted to equivlalence an array containing 3,334 numbers, you'd need a string DIMensioned to (6 x 3,334) or 20,004.
TIMING
The program also times itself. The first column of entries in Figure 1 is for my own disk drive--a single density Indus GT. The times you get may be different if you use a different brand of disk drive. The second column in Figure 1 contains run times for a RAMdisk.
The first entry in Figure 1 is the number of seconds it takes to write 3,334 elements (20,004 bytes) from M() to a disk file named D1:ARRAY.DAT. If the same data gets written as a 20,004-byte string to a disk file named D1:STRING.DAT, the run time decreases from 99.03 seconds to 83.95 seconds. If you write the data to RAMdisk files, writing to the string is almost ten times faster than writing to the floating-point array, 53.58 seconds and 5.73 seconds, respectively.
The increase in the speed of initializing the arrays is even more impressive. Ordinarily you'd initialize a floating-point array with a FOR-NEXT loop, such as in line 540 of Listing 2.
You can do the same thing with an equivalenced string in two quick steps. Assign the first element the regular way, M(0)=-1. Since S$ is equivalenced to M( ), this assignment will also change the first six bytes of S$.
Now you can copy the first six bytes throughout the rest of the string with the statement:
S$(7)=S$(1)
This statement will change every value in M( ) to -1. The equivalenced string method is 120 times faster than the FOR-NEXT loop for an array of 3,334 elements.
The bad news is that BASIC lacks a speedy way to read D1:STRING.DAT back into S$. So we resort to a little machine language.
The subroutine beginning at line 3000 in Listing 2 uses your Atari's built-in CIO (Central Input/Output) routines to read a disk file into a string at machine language speed.
In this routine, AD is address of the string. It is broken into low- and high- bytes in line 3000. The expression POKE I+8,255:POKE I+9,255 tells CIO to read as many bytes as it can, up to 65,535 bytes, or until it reaches the end of the file. Line 3030 contains the USR function which starts the CIO routines. When CIO is through, line 3040 calculates the number of bytes which have been read and stores it in N.
To learn more about CIO, read the CIOV section (location 58454) of Ian Chadwick's "Mapping The Atari" ($16.95, Compute! Publications).
TURBO BASIC XL
If you own an XL or XE, Turbo BASIC XL also has the fast I/O commands you need.
Turbo BASIC XL is by Frank Oztrowski, of West Germany, author of Michtron's GFA BASIC for the Atari ST. Turbo is a public domain BASIC interpreter and compiler that offers a more powerful programming environment. It's available on CompuServe's 8-bit Atari Forum and from many Atari users groups.
Turbo BASIC supports structured programming, provides new I/O, editing, and DOS functions, and RUNS several times faster than Atari BASIC. Unfortunately, it does not work on Atari 400 or 800 computers.
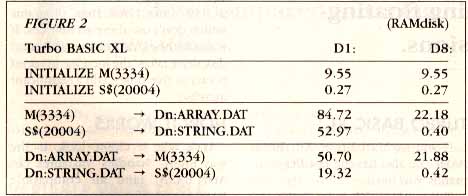
Turbo BASIC XL has %GET and %PUT commands to read and write numeric data to and from disk, and BGET and BPUT to read and write string data to and from disk. Substituting these commands for the Atari BASIC commands in Listing 2 will give you the run times listed in Figure 2. The Turbo BASIC commands and their Atari BASIC equivalents are in lines 630-640, 730-740, 1070-1080 and 1200-1210.
Turbo BASIC is somewhat faster than Atari BASIC for the floating-point routines. Reading into S$ from RAMdisk or writing S$ to RAMdisk takes only four tenths of a second in Turbo BASIC! If the string is a little smaller, such as 8,138 bytes (the size of a GRAPHICS 8 screen & display list) the read and write times are less than two tenths of a second. Reading or writing a GRAPHICS 0 screen (992 bytes) to or from RAMdisk takes one tenth of a second.
The net effect is that programs using Turbo BASIC, RAMdisks and equivalencing will transfer data 130 to 150 times faster than programs which don't use these techniques. If you add the extra time that a physical disk drive takes, the increase in speed is two to five times, still a significant increase.
HOW IT WORKS
Let's take a closer look at the way BASIC handles variables. In AtariBASIC (and all compatible BASICs) variables are stored in tables. The three tables of interest here are the variable name table, the variable value table, and the string and array table.
VARIABLE NAME TABLE
The variable name table is merely a list of all of the names of the variables used in your program. Instead of putting a space between the variable names (and wasting a byte), the last character in each name is stored as an inverse character. If our program contains the variables- TOTAL, ARRAY(5), and NAME$(10)--the variable name table would look like this:

Atari BASIC recognizes three classes of variables--scalars, floating-point arrays and strings. If the last character in the variable name is an inverse letter or number, as in TOTAL, the variable is a simple floating-point number called a scalar.
If the last character is an inverse open parenthesis, as in ARRAY, the variable is a floating-point array. And if the last character is an inverse dollar sign, as in NAME$, it is a string variable.
The address of the beginning of the variable name table is stored in memory locations 130 (low byte) and 131 (high byte). Calculate the starting address of this table with the equation:
PEEK(130) + PEEK(131) * 256
The ending address of the variable name table is one less than the number stored in memory locations 132 and 133.
VARIABLE VALUE TABLE
The variable value table contains: type and size information about each variable. The starting address of the variable value table is kept in memory locations 134 and 135.
Each variable in the variable name table has a corresponding eight-byte block of information in the variable value table. These blocks are kept in the same order as the names in the variable name table.
The first byte in each block represents the variable type. A 0 represents a scalar, 64 and 65 denote floating-point arrays, and a 128 or a 129 represent a string variable.
The second byte of each block is the variable number (0--127) as assigned by BASIC.
If the variable is a scalar, the remaining six bytes contain its binary coded decimal (BCU) value, as described above.
If the variable is a floating-point array or a string, the third and fourth bytes contain the location of the array (or string). This location is not a memory address, but its offset into a table containing all the strings and arrays used in your program. This table, called the string and array table, is discussed later in this article.
If the variable is a floating-point array, the fifth and sixth bytes are equal to one plus the first DIMension size, and bytes seven and eight are equal to one plus the second DIMension size.
For example, the statement DIM ARRAY(7,13) would set bytes five and six equal to 7 +1, or 8, and bytes seven and eight would equal 13 +1, or 14. (If ARRAY was a one-dimensional array, bytes 7 and 8 would equal 0+1, or 1.)
If the variable is a string, the fifth and sixth bytes contain the current length of the string. The seventh and eighth bytes contain the DIMensioned size of the string. For example, when processes the statement DIM NAMES$(10), it sets bytes five and six to zero because the LENgth of NAME$ is zero. (Bytes five and six remain at zero until your program puts something into NAME$.)
Bytes seven and eight would equal ten, the DIMensioned size of the string.
STRING & ARRAY TABLE
The string and array table contains the contents of all the strings and arrays used in your program. The starting address of this table is kept in memory locations 140 and 141.
Each time your program introduces a new string or array, its contents are appended to the string and array table. BASIC keeps track of these variables by noting their offset from the beginning of the string and army table, and storing this number in the variable value table.
In other words, the first array is located at the beginning of the string and array table and has an offset of zero. The second array's offset would be equal to the size of the first array.
HOW TO EQUIVALENCE
These variable tables let BASIC give each variable a unique set of data that points to a unique area ofRAM. When you equivalence two variables, you manipulate these tables so that the two variables share the same area of RAM. Scalars, arrays, and strings may be equivalenced in any combination, as long as the equivalenced memory locations do not overlap other variables.
Once you understand how the variable tables work, equivalencing is merely a matter of altering the eight-byte blocks in the variable value table. Just copy the array's offset and dimension information into the offset and dimension information of the string. Here's an example:
NEW
DIM A$(1),B(2)
After BASIC processes these statements, the variable name table will look like this:

And the variable value table will look like this:

Which is equivalent to:
129 0 0 0 0 0 1 0
(entry for A$)
65 1 1 0 3 0 1 0
(entry for B())
Let's interpret each eight-byte block. In the first block, the first byte, a 129, tells us that the variable is a string. The second byte, a 0, means that it is variable number 0--the first variable in your program. It also means it's the first entry in the variable name table, A$.
Bytes three and four, also zeros, mean that its offset from the beginning of the string and array table is zero.
Since no elements have been entered, A$ has a LENgth of 0 (bytes 5 and 6 = 0), but has been DIMensioned to 1 (byte 7 = 1 and byte 8 = 0).
The second block contains information about the second variable. Here, the first byte, a 65, tells us that the variable is a numeric array. The second byte, a 1, means that it is variable number 1--the second variable in your program. It also means it's the second entry in the variable name table, B( ).
Bytes three and four, a one and a zero, mean that the B( ) offset from the beginning of the string and array table is one--the maximum size of the previous variable A$.
Bytes five through eight contain the variable's DIMensioned size. BASIC arrays may have up to two indexes, and both sizes are stored here. Bytes five and six show the DIMensioned size of the first index + 1. Bytes seven and eight show the DIMensioned size of the second index + 1.
In this example, the DIMensioned size of the first index is 2. Byte five contains (2 + 1), or 3, and byte six contains zero.
Since there is no second index, its value is 0. Byte seven contains (0 + 1), or 1, and byte eight contains zero.
To equivalence A$ and B( ), copy bytes three through eight of block two into bytes three through eight of block one. The variable value table will now look like this:
129 0 1 0 18 0 18 0
(entry for A$)
65 1 10 30 10
(entry for B ( ))
Block two has not changed, but block one now points to the same memory locations as block two. Both now have the same offset into the string and array table.
You'll notice that bytes five through eight were not copied as you'd have expected. These bytes, describing the DIMensioned size of the array, appears to have jumped from 3 to 18!
Nothing's really changed, though. As an array, B( ) may hold up to three floating point numbers. Since your Atari needs six bytes to store 1 single floating point number, it needs 18 bytes to store three of them. Thus, if A$ and B( ) are to use the same piece of RAM, A$ must be 18 bytes long.
Since A$ and B( ) now occupy the same 18 memory locations, any change in A$ will affect B( ) and vice versa.
Substring Array Element
A$( 1, 6) <-----> B(0)
A$( 7, 12) <----> B(1)
A$(13,18) <----> B(2)
A$ was originally DIMensioned for one element for the sake of simplicity. If A$ had a DIMension of 600, its new offset would be 600 after equivalencing.
Bytes 0 to 599 of the string and array table would be inaccessible memory.
Inaccessible memory A$ and B( ) stored here
________________ __________________
Bytes 0 to 599 600 to 617
If you don't like wasting this much memory, you can alter the variable value table so that the offset and DIMensions of both A$ and B( ) include all 618 bytes.A$ would then have a DIMension of 600 + 3 * 6, or 618. B( ) would have a DIMension of 600/6 + 3, or 103. Wasting memory will usually not affect your program. However, you should be aware of some potential problems with equivalenced variables.
POTENTIAL PROBLEMS
Losing your place. This happens when you incorrectly equivalence your variables. This can happen when creating the equivalence, or whenever the program processes a misplaced CLR statement.
A CLR statement zeroes all of the variables and sets the offsets, string lengths, and array dimensions to zero in the variable value table. The equivalence between variables is destroyed.
When you re-dimension the strings and arrays, BASIC once more assigns a unique offset for each. Each variable will control its own part of memory again.
Finally, remember that the order of your variables in the variable tables is subject to change whenever you LIST your program to disk. The SAVE/LOAD commands preserve your program's original variable name table. The LIST/ENTER commands do not. When a LISTed program is ENTERed, BASIC builds a new variable name table. Be sure your program knows how to search through the variable tables for the information it needs.
OTHER USES
The previous examples mostly speed disk I/O. But there are many other powerful ways to use equivalenced variables, such as creating and manipulating pseudo-records and defining pointers.
Pascal lets you to declare RECORD data types. A RECORD is a variable which contains other variables. For example, a single RECORD variable for a banking program might contain a person's name (a string), an account number (an integer), and account balance (a floating-point number).
You can emulate a RECORD in BASIC by consecutively equivalencing a set of variables into one large string.
This form may be useful for creating a small database or other systems where you need to keep data grouped together in a particular fashion.
You can also use equivalenced variables to emulate pointers. Just find the string's eight-byte block in the variable value table and change its offset (bytes three and four) to point to the desired memory location. In Listing 1, for example, we made the string point to the audio control registers.
Try some high-speed screen I/O. Create a string the same size as the screen and point it to screen memory. Anything you put in the string will appear onscreen instantly.
PROGRAM TAKE-APARTS
Listing 1 equivalences a string with the audio control registers, memory locations 53760-53767. S$ is an eight byte string that is offset so that it points to those locations. CH$ contains the frequency, distortion, and volume values for each of the eight audio control registers.
The first part of Listing 1 takes the frequency, distortion, and volume value from CH$ and puts them into the SOUND command.
You could speed up this routine by storing these values in an array. This would avoid the string-to-floating-point conversions, but would require 4,608 bytes of memory instead of 256 bytes (nine times more space) and would still be slower than the second part of the program.
In the second part, the program sets S$ as a pointer to the audio control registers. They are set very quickly by copying eight-byte substrings of CH$ into S$.
Listing 2 demonstrates the generalized method for equivalencing variables. As written, it can be RUN in Atari BASIC or Turbo BASIC XL.
Listing 2 begins by asking the size of the floating-point array M( ). After DIMensioning M( ) and the string variables, Listing 2 finds the location of each of the variable tables.
Next, the program jumps to the subroutine at line 2000 to find the variable number, offset and dimensions of M( ) and S$. The actual equivalencing of M( ) and S$ occurs in lines 380-500. Lines 520-1250 contain the I/O and initialization benchmarks for the data in Figure 1 and Figure 2.
The subroutine at line 1500 contains a timer and the subroutine at line 1600 prints the first five elements of M( ) to show that the contents of M( ) actually do change during the benchmark routines.
Doug White of Arlington, Texas uses his 1200XL as an aid in designing and testing loudspeakers. This is his first appearance in Antic.
Listing 1: EQUIV1.BAS Download
Listing 2: EQUIV2.BAS Download