GRAPH 3D
Spectacular three-dimensional visuals!
by PAUL CHABOTExplore the world of visual calculus and create three-dimensional graphs from mathematical functions. This BASIC program will run on all Atari computers with 48K memory and a disk drive.
If you've seen the fantastic, computer-generated
landscapes in movies such as "The Last Starfighter," you know what a three-dimensional
graph looks like. Graph 3D creates three-dimensional objects in Graphics
Mode 8, based upon functions of the form: Z = f(X,Y). Your landscapes,
or objects will not be solid, but you can alter the density of the graph
lines.
The second part of this article will cover technical details,
but you don't need a degree in calculus to create shapes with Graph 3D.
Here's how to get it up and running.
GETTING STARTED
Type in Listings 1 and 2 and check them with TYPO II. There's some
machine language in these programs, so make sure that your TYPO II codes
are correct and that you haven't left out any lines. SAVE Listing 1 as
GR3DLOAD.BAS. Since Listing 1 automatically runs Listing 2, be sure and
SAVE Listing 2 as GRAPH3D.BAS and don't try to run GRAPH3D.BAS by itself.
Those using Antic's DISKIO (January, 1985) should boot these programs without
it.
Run the program GR3DLOAD.BAS. First a title and then a
menu will appear. After a brief pause, a black graphics screen will take
its place and begin drawing a sample graph. When the graph is completed,
the menu will retum. You can switch between the menu and the graphics screen
by pressing [SPACE]. The commands on the menu are single letter options
which can be used from either the screen or the menu. Choose a command
option by pressing the letter with no [RETURN].
For example, let's SAVE the picture that's currently on
the screen. Be sure there's a disk with 62 free sectors in Drive 1. Type
[5] and, at the prompt, type in the filename and then press [RETURN] and
answer [Y]. You don't need the D: device prefix and Graph 3D will automatically
add an extender of .G3D. For the technically oriented, Graph 3D files are
straight Graphics 8 + 16 picture files consisting of 7680 bytes of screen
data followed by 13 records contaming parameter information. (See lines
910-918.)
ENTERING A FUNCTION
Let's type in a function without worrying about why it works. (We'll
save that for later.) Get to the menu by pressing [SPACE], if you're not
already there. Type [F] for function. You should see the current function
and under it, Z =. Now type 1-2 * Y * Y and press [RETURN]. Next, type
[E] for eye placement, then type 10,10,5 [RETURN]. Set the magnification
to 120 by typing [M] [120] [RETURN]. Center the graph by typing [C] [160]
[RETURN] [30] [RETURN]. Finally, type [I] and enter -2,2,-1,1 [RETURN].
Now, to graph the object to the screen, press [G]. Parts
of the menu will flash and you'll see the message "Computing Points." The
graphics screen will then appear and begin drawing an object that should
end up looking like a trellis tunnel.
ALTERED STATES
Many of the menu choices in GRAPH 3D alter the view of the displayed
object. In most cases, you must press [G] to redraw the object using the
new values. The best way to understand any of the commands is to try different
values, press [G], then examine the results.
Our example shows [M] will change the magnification of
the graph and [C] will shift it on screen by entering new X and Y coordinates
based upon the usual screen grid where 0,0 is the upper left corner.
[E] is the eye location in three-dimensional space. Place
a square grid on the floor and the two directions of the grid are X and
Y. A pole running perpendicular from the floor is the Z axis, and the three
values entered are in order: x,y,z.
You can change the number of X and Y cross-grid lines
with [N]. High values give more detail to the surface but require more
computing time. The maximum value allowed is 24.
[O] when pressed, increments the graphing option. Various
features of the surface can be accentuated by showing some cross-sections
and not others. The options are:
0-all available cross-sections graphed.
1-all X sections, only first and last Y section.
2-all Y sections, only first and last X section.
3-all X sections, every third Y section.
4-all Y sections, every third X section.
5-every third cross-section.
If you wish to alter these options, see lines 306-3 18 and 522.
The two intervals defining the rectangular region under
the graph can be altered with [I]. These will show up in square brackets
on the screen, but should be entered in order AX,BX,AY,BY
[F] permits you to enter a new function. If your object
ends up a complete mess, have no fear! Press [R] and you may restore your
previous graph which has been saved in memory.
[R] will also work after a graph file has been loaded
with the [L] command. The [L] command, which loads a previously saved picture
file, is similar to the [5] save command in that you only need to enter
the name and the computer will provide the device and .G3D extender.
[D] will search the disk for any files with .G3D extenders
and display them in the menu directory.
[P] is a screen dump designed to print the graphics screen
to your printer. It is designed for a Gemini l0X but the routine, which
begins at line 960, could be altered for your own printer. (For a much
faster screen dump that will work on various printers and can be used with
Graph 3D files, see "Kwik Dump" by Jerry Allen, Antic, March, 1985
-ANTIC
ED.)
TECHNICAL INFO
Each point (P) in three-dimensional space is determined by a "triple"
(X,Y, and Z coordinates). The first two coordinates specify a spot in the
usual X,Y plane, which is visualized as lying on the floor. The third coordinate
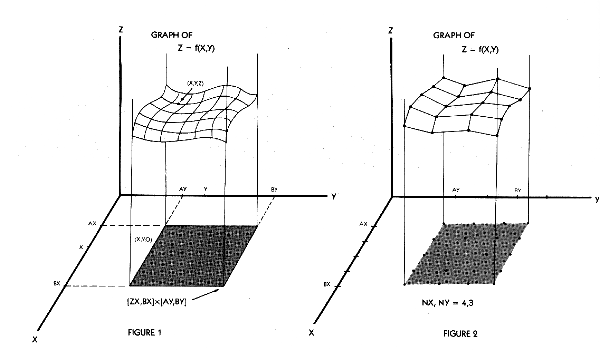
gives the distance of P above or below this spot. Figure 1 shows
the usual orientation of the three axes.
The graph of a function Z = f(X,Y) is the collection of
all triples, where the third coordinate, Z, is computed from the first
two using the function f. For example, the graph of Z=X*X+Y*Y contains
points like (1,1,2), (2,3,13), (-1,2,5) since each of these satisfy the
equation. Specifically, the third coordinates are all obtained from the
first two by using the rule Z=X*X+Y*Y Such graphs are visualized as surfaces
in three-dimensional space.
Obviously we cannot draw the entire graph of a function.
Graph 3D sketches only portions of graphs. Figure 1 depicts a typical
situation. Along the X-axis we have the interval [AX,BX]. Along the Y axis
you'll see the interval [AY,BY]. Together these describe the rectangular
region [AX,BX]x[AY,BY1 This consists of all pairs X,Y with AX< = X<
= BX and AY<=Y<= BY. Above each spot in this region there is a point
on the graph. The third coordinate Z is found by evaluating f(X,Y). It
is also clear that we can't do this for every possible X,Y in the region.
This is where the partition sizes NX,NY come into play
Figure
2 shows a 4,3 partitioning. With NX = 4 the interval [AX,BX] along
the X-axis is broken into 4 equal pieces (subintervals). Whereas the Y
axis interval [AY,BY] is split into 3 subintervals. This leads to 20 spots
of interest in the rectangular region. The function f(X,Y) is then computed
at each of these, resulting in 20 data points actually on the graph. We
now connect these with line segments to get a rough idea of the shape of
the graph.
Larger values of NX,NY will give you a better looking
picture but will take more time. Also, if you plot too many data points
and joining line segments, your picture can quickly become cluttered. This
is solved with the graphing options [O].
FUNCTIONS TO TRY
To get you started here's a list of functions with suggested rectangular
domain and eye location. When you build up the courage to try your own
just be careful to avoid the "value error" trap. Be sure that the function
you use is defined on the entire rectangular region. Graph 3D will accept
each of the following examples. Use the menu selections [F], [I], and [E]
to input the data.
1. Z=1-2*X*X
[-2,2]x[-1 ,1] eye:1 0,10,5
2. Z=X*X+2*y*y
[-1,1]x[-1,1] eye:10,14 4
3. Z=SIN(3*X)
[-1,1]x[-1,1] eye:10,15,12
4. Z=SQR(X*X+3*Y*Y)
[-3,3]x[-1 ,l] eye:1 0,2,3
5. Z=EXP(-X*X-Y*Y)
[-2,2]x[-1 ,1] eye:4,10,3
6. Z=4*X*X*X*X-4*X*X+y*y
[-1,1 ]x[-1 ,1] eye:1 0,17,4
7. Z=1/(0.5+X*X+Y*Y)-1/(0.5+X*X+(Y-2)*(y-2))
[-2,2]x[-2,4] eye:20,1 0,10
8. Z=COS(3*X*Y)
[-1 ,1 ]x[-2,2] eye:20,1 0,40
9. EXP(SIN(X*Y))
[-3,3]x[-3,3] eye:1 0,20,30
10. Z=X*X*X+2*Y*y*y
[-1,1]x[-1,1] eye:10,10,5
You'll find the 3D graphs of some of these functions illustrating the article. If you create an impressive new function, be sure to send it to Antic as an I/O Board letter.
Paul Chabot, professor of mathematics and computer science at California State University, Los Angeles, returns to BASIC here after publishing ACTION! graphics programs in the April and June, 1985 issues of Antic.
Listing 1 GR3DLOAD.BAS Download
Listing 2 GRAPH3D.BAS Download