PROGRAMMING
Assembly Line
NUMBERS, PART I
by Douglas Weir

I think that now is a good time to start talking about numbers. As we've seen, the 68000 at the lowest level works only with numbers; so it's more than a little ironic that the assembly-language programmer usually has to go to much more trouble to write even simple number-crunching programs than he or she would for string manipulation programs.
Much of the problem, of course, lies in handling the I/O. The "numbers" typed at the keyboard have to be translated from character strings into integral binary values that can be added, subtracted, multiplied, or whatever; and when it comes time to output the results of these calculations, the numbers have to be translated back into character strings. There's a lot more to this than meets the eye, and it's one reason why routines like print() in C are large and complicated. This month we'll take a look at converting unsigned integers back and forth, and in the process learn something about multiplication in the 68000.
This is something of a chicken-and-egg situation. We could write math routines to our hearts' content, but we'd have no idea how accurate the routines were unless we could look at (i.e., output) the results. But it turns out that the routines required for input and output require a fair amount of computation themselves, so writing a set of conversion routines is a good first step in more ways than one. This month's program does nothing more than repeatedly input two integer strings from the keyboard, convert them into binary values, multiply them, convert the result into a string, and print it. This, however, requires a lot of multiplication and division. Let's see how it's done.
The awful truth about multiplication
Let's think 32 bits. We know that the 68000's data registers are 32 bits long, so it seems reasonable to assume that we can multiply numbers up to 32 bits long with the 68000's multiply instruction.
Unfortunately, this is not a correct assumption. The 68000 does indeed have a multiplication instruction, but it can handle operands only up to 16 bits long. This is because multiplying two numbers almost always produces a result with more digits than either of the operands; in fact, the operand can be as much as twice as long as two equal-length operands. This is just as true of decimal numbers as it is of binary; for example, 99 * 99 = 9801. Since the result of the multiply instruction is stored in a single-data register, it's clear that neither operand can be greater than 16 bits. In other words, if you are multiplying unsigned integers, the largest operand you can have is 65535.
Note that it's perfectly possible to have one operand much longer than 16 bits and still come out with a product that could be held in 32 bits, as long as the other operand was small enough. For example, 99999 * 1 = 99999, which is only 17 bits long. Nevertheless, you can't do this example on the 68000 without writing some routines of your own, because of the arbitrary restriction of 16-bit operands. This month we will take the first step toward writing a general multiple-precision multiplication routine. For now, we want to have the ability to multiply any pair of integral numbers, no matter what their sizes, so long as their product doesn't exceed the 32-bit limit.
Now let's take a look at the 68000's mulu (multiply unsigned) instruction, which will be the basis of our routine. In order to multiply two unsigned 16-bit (or smaller) integers using this instruction, you load each operand into the low word of a data register, and then specify these two registers as the source and destination of the instruction. For example:
move .w #1685, d0 move .w #1756, d1 mulu d0, d1 |
In these three lines of code, the integers 1685 and 1756 are multiplied. The 68000 puts the product of the multiplication into the destination register. In other words, the original contents of the destination register are always lost when a mulu is executed. Since the product can be up to 32 bits long, all 32 bits of the destination register are written to by mulu.
The ideal multiply
What we would like to do is multiply the entire contents of two 32-bit registers, thus obtaining a 64-bit product. For the time being, we'll ignore the "high" 32 bits of such a product, and just trust ourselves to choose only those pairs of operands whose products won't exceed 32 bits in length. This is analogous to multiplying decimal numbers with, say, two decimal places each instead of one decimal place.
With decimal numbers, multiplying single-place integers is easy, assuming you know your multiplication tables. For example, 9 * 9 = 81, 4 * 6 = 24, and so on. To multiply a couple of two-digit numbers, we usually need a pencil and paper:
24 * 48 ----- 32 (8 * 4) 16 (8 * 2) 16 (4 * 4) 8 (4 * 2) ----- 1152 |
Here, a series of partial products is added to get a final product. Doing the partial products lets us multiply larger numbers as if they were made up of smaller ones; we sort of ignore the extra decimal places, but everything comes out all right in the end because of the way the partial products are grouped and added. Thus, the partial product 8 * 2 is written beginning in the 10's column, since the 2 is actually a 20; and so on.
We can use this same technique to multiply the contents of the 68000's binary data registers. Suppose we wanted to multiply the contents of registers d5 and d6. Without bothering about the actual configuration of bits in the registers, we can imagine the numbers in them being arranged as in Figure 1, where each of the two registers is made up of a "high" word (16 bits) and a "low" word, represented by H and L, respectively.
FIGURE 1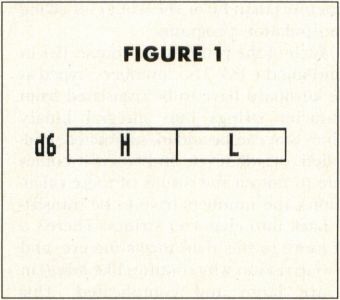
What we need to do
In a normal 68000 mulu operation, only the two L portions of the registers would be multiplied, much as the rightmost digits of 24 and 48 were multiplied in the decimal example above. If we want to write a routine to multiply all 32 bits of both registers, then we have to do much the same thing as we did with the two-digit decimal numbers. First we must multiply d5's low word with d6's low word; then d6's low word with d5's high word (and we must remember to add this partial product in at the right binary digit place, just as we did with the decimal product); then d6's high word with d5's low word; and finally, the two high words of d5 and d6. The sum of all these partial products, correctly done, will be the full 64-bit product of the two 32-bit registers. The arrangement of the partial products for the final sum would look something like Figure 2.
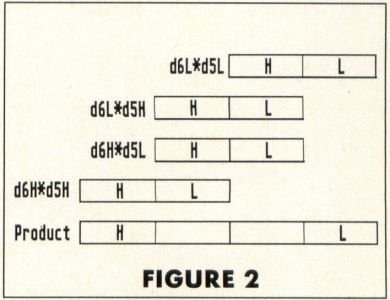
In other words, suppose we've reserved eight bytes of memory for the product of the two registers. We now multiply the low words of the two registers, and store the result in the low longword of our storage area. Next we multiply the low word of d6 with the high word of d5. We add this result to the "middle" longword of our storage area. Likewise with the next partial product (from the high word of d6 and the low word of d5). Finally, we add the last partial product (from the two high words of the registers) to the high longword of the storage area.
This month's program
And that's just what the routine mul32 in this month's program does. It receives its two 32-bit operands on the stack, multiplies them, and replaces the operands with the 64-bit product, so that the caller can simply pop it off the stack after the subroutine returns.
Let's look at mul32 in more detail. After clearing several data registers, I load register a1 with the base address of a table of addresses of three tiny subroutines—I'll explain what these do a little later on. I load the two operands from the stack into data registers d5 and d6, and load the address of the "top" operand (i.e., the first pushed, and thus the higher in memory) into register a0. To do this, I used a new instruction, lea (load effective address).
We discussed the concept of "effective address" several installments ago. In essence, the effective address of an operand can be said to be "where the processor goes to get the value for the operand." The lea instruction simply calculates the address for the operand in the source field, and loads this address (not the operand) into the destination operand. Here, the effect of lea is that a0 is loaded with the address of the first of the two operands pushed. The next two instructions clear the 64-bit area originally occupied by the operands; this is where the product will be returned.
It's actually quite easy to get at the high and low words of the two operands in order to calculate the partial products. The 68000 swap instruction exchanges the 16-bit halves of any data register, making the high word the low, and vice versa. Once we have the correct word in the bottom half of the register, it can be multiplied with mulu. However, since mulu always destroys the original contents of its destination register, we need to move the current word-operands into a set of "temporary" registers for the actual computation.
This is done at the top of m__loop. The low words of d5 and d6 are moved into d2 and d3 and multiplied. Now comes some special checking. Remember, we're adding these partial products into a cumulative total. That means we have to keep in mind the possibility of a carry from the previous addition. This occurs in much the same circumstances that it would in decimal addition. If, for example, we were to add 19 + 19, then we would first add the two 9s, get 18, and write the 8 in the 1's column. The 1 would be carried over into the 10's column and added in with the two 1s there.
Carrying on in binary
When, for instance, two 1s are added in binary arithmetic, the following happens:
1 ( 1 decimal) +1 (+1 decimal) ---- 10 (2 decimal)
Here, a zero is entered in the current place, and the one is carried over one place. Obviously, this sort of carry occurs quite often in binary arithmetic, and the process of carrying the ones over is completely transparent to the programmer—unless the bit from which the one is carried happens to be the leftmost bit of the data size of the operand. In other words, imagine what happens if you add the low word contents of two registers and there is a carry out of the 16th (i.e., leftmost, since this is a word) bit of the result. In this case, the bit has nowhere to go, and the programmer has to be warned.
This warning is accomplished by setting the Carry flag in the Condition Codes register. Whenever we add a partial product to our cumulative sum, the Carry flag will be set if there has been a carry out of the leftmost bit of the destination. So we have an easy way of finding out about carries. However, it's not so convenient to do anything about it at the moment it's detected. Why not? Because the carry will have to be added into the next part of the sum, and we haven't gotten to it yet. So we have to save the condition, since, as we know, the Condition Codes change constantly, almost with every instruction. Fortunately, there's a very simple way to do this.
If you look down a few lines to the next label, you'll see (under the add) the instruction scs. This is just one form of a versatile instruction that allows you to save any condition in a specified destination. Here scs means "set if carry set." If the Carry flag is set when this instruction is executed, then the destination (always byte-sized) will be loaded with all 1s; i.e., all bits of the destination byte will be set if the Carry flag is currently set. If the Carry flag is not set, the destination will be cleared (loaded with 0s). This instruction is listed as sec (set according to condition) in the manuals, similar to bec (the branch instructions). There you can find the correct form of the instruction to save whatever condition you want.
Now let's return to the instruction after mulu. The instruction tst simply "tests" the contents of its operand and sets the Condition Codes accordingly. After testing d4, we can find out if a previous carry has been saved in it or not. If d4 contains zero, then there was no carry, and execution proceeds to the label, m__nxt0; otherwise, 1 is added to the current partial product which will be added to the cumulative sum.
Adding the products
In fact, this addition is the next thing that is done. The double longword into which we are adding the products is indexed with the register d0. The first time through this loop, a0 is pointing to the low longword and d0 contains zero, so the first partial product goes into the low longword of the product. The next couple of times, we want to add into the "middle" longword of the product. This is done by subtracting two from d0. With the indexed addressing, this is the same as subtracting two from the address in a0 and thus pointing one word left or "higher up" in the product. The last partial product is added into the high long-word, and we point to it by again subtracting two from d0.
How do we know when to subtract from d0? We don't want to do it on every iteration—the second and third partial products have to be added into the same longword area. Since it turns out that we want to subtract on odd iterations (the first and third) only, all we have to do is find out if we're on an odd iteration, and if so, subtract. This is done with our next-to-last new instruction, btst.
The btst instruction allows you to test the state of any single bit in the destination operand. The number of the bit (counting from 0 as the rightmost bit) can be specified as an immediate value, as it is here, or it can be contained in a register. If the bit is set, then the Zero flag in the Condition Codes register will be cleared. If the bit is not set, then the Zero flag will be set.
After counting the loop in d1, I test d1's rightmost bit. From our binary arithmetic, we know that each bit in a register stands for a power of two, counting from the rightmost bit. Bit 0, then, (the bit we are testing), stands for the value of two to the zero power, i.e., 1. This is the only power of two with an odd value, so if this bit is set, we know that the register as a whole contains an odd value. So, after doing the btst, the Zero flag will be cleared if d1's rightmost bit is set, the beq will not be executed, and the immediate value 2 will be subtracted from d0. If the bit isn't set, then the branch will be taken, and the subtract from d0 will be skipped this time.
The indirect jump
Finally, we have to do some swapping of d5 and d6 on every iteration in order to get the desired partial products. This is handled with the trio of tiny subroutines m__swap__1, m__swap__2 and m__swap_3. Remember that we loaded the base address of a table which contains the addresses of these routines into a1 at the beginning of the routine. Since each address in the table is four bytes long, we can index through this array of addresses by adding offsets of 4 to the value of a1. Each time through the loop, the next subroutine address is indexed and loaded into a2.
The address now contained in a2 is essentially the same thing as the label that identifies a subroutine in the destination field of a bsr instruction: The label is, as we know, really an address. We can "jump" to the address contained in any address register by executing the jsr (jump to subroutine) instruction. You can't use the bsr instruction here—I'll explain why next time.
Thus, on every iteration of the loop, we index to the address of a subroutine that contains the correct swap instructions to set up the data registers for the next mulu, and we then execute that subroutine by "jumping" to the value in a2 "indirect." (We're jumping to the address contained in a2—hence the parentheses—not to a2 itself!) As part of its operation, jsr pushes the return address onto the stack, just as bsr does. Thus a simple rts at the end of each subroutine returns us to the next instruction after the jsr.
And that's just about all there is to it. When mul32 terminates, its caller can pop the high and low longwords of the product off the stack. The caller would have to adjust the stack anyway, since that's where the operands were passed in the first place, so not much time and no space is wasted.
Next time
We'll look at the rest of this program in detail next month. In the meantime, type in the source code and assemble it. When run, the program will wait for you to type in two numbers, each followed by a carriage return. After you've entered the second number, the program will multiply them and display the answer. You can repeat this process as often as you like—the program won't terminate until you press CONTROL-C. If you type a number that's too large for the program to handle, or if the product of two numbers is too large, the program will display an error message (the message is the same in all cases), and terminate.
And now I have a small confession to make. The version of mul32 given here is probably not the simplest way to do 32-bit multiplication, but I took advantage of the opportunity to introduce some little-used instructions. You can try your hand at other methods—just rewrite the subroutine to your taste, and as long as it receives its operands and returns its answer in the same way as the original version, it should work fine with the other routines (don't forget to save and restore at the beginning and end of your routine all the registers you use). As for the approach you should take, here's a hint: Try not using a loop.