Opus
by Doug Harrison
Whether you're a businessperson forecasting profits, a scientist analyzing data, or the average guy trying to figure out where all his money's going, there's no doubt about it—you can solve these problems and many more with a spreadsheet program. A spreadsheet presents you with a large array of cells, and each cell can hold a number, label, or formula. Formulas allow you to reference values held in other cells, so you may add them, subtract them, etc., and you may also supply them to various functions such as SUM, FV, and LINR. This makes it easy to construct complicated models with a minimum of effort, and you can change a value and instantly observe the effect on cells that depend on it (a game called "what if").
Meet Opus, a fully GEM-based, 999 row by 255 column spreadsheet written wholly in Personal Pascal from OSS featuring sparse matrix design, flexible on-screen formatting with WYSIWYG printer output, more than forty functions, natural order recalculation, expandability through the GEM message pipeline, genuine ease of use, comprehensive error trapping, and much more. In the following pages, I'll more or less explain the operation of the program for the spreadsheet novice, but when relative, I'll also try to describe why certain things are done the way they are. And next month, I'll discuss some items of interest to programmers.
Getting started
Due to the huge size of this program, it is impossible to supply program listings in the magazine. You may get your copy of Opus by purchasing this month's disk version, or by downloading the program from the ST-Log SIG on DELPHI.
The complete program consists of the following files: OPUS.PRG, OPUSM.RSC, OPUSH.RSC, PRINTER.INF, INSTALL. PRG, INSTALL.RSC, and several files with the extender "OPS," which are sample worksheet files in OPUS format. OPUS. PRG is, of course, the worksheet program; OPUSM.RSC is the resource file for medium resolution; OPUSH.RSC is the resource for high resolution; and PRINTER.INF is a printer configuration file for EPSON-compatible printers. INSIALL.PRG allows you to create a printer driver for non-compatible printers and is fully self-explanatory when run. However, you will be required to research your printer's control codes, which should be listed in the printer manual.
You may transfer the Opus files to any folder and hard disk partition, as long as they all reside in the same directory (the OPS files may be placed in any directory). Color monitor owners should make sure they are in medium resolution before running Opus. As Opus is a fairly large program, owners of 520STs with the standard 512K should make sure they haven't booted with accessories requiring great amounts of memory, although the Control Panel and many others are certainly not a problem; the only real way to tell if an accessory is too large is to experiment.
Double-click on OPUS.PRG; the program will first load its resource file and then PRINTER.INF. Should it fail to find OPUS(M/H).RSC, the program will terminate with a message; should it fail to find PRINTER.INF, you will be informed that any printing will be done without the special codes needed for italic print, NLQ, etc., and Opus will otherwise run normally.
First impressions
Opus initially greets you with a typical GEM display, consisting of the menu bar, a "control panel" and a single window. Opus's control panel contains, from left to right, the cell name of the active cell, a pulldown menu area from which you may select functions, the cell-delete icon, the data-entry icon, and the edit area. Items to note in the worksheet window include the row and column titles and the "cell-cursor," which initially is found in the upper-left cell or "home" cell.
Cells are identified by combining the column letter(s) with the row numbers; thus, the first cell is written as "A1." Other examples of valid cell references are Q950, CA1, DZ25, and $A$1 (more on the "$" later). The control panel will always display the location of the cell-cursor—that is, the name of the "active" cell. The characters you type appear in the edit area, and you enter data into the active cell by terminating your entry with any of the four cursor keys, Return or Enter, or by clicking on the data entry icon (the one with the checkmark). Naturally, the cursor keys assign a value to the active cell and then move in the appropriate direction if possible, activating the adjacent cell, while Return, Enter, and the entry icon all assign a value to the active cell without moving, unless the cell-cursor is within a block and ";Auto Cursor" is selected (more on that later).
You may have noticed that Opus is presently ignoring certain keystrokes, specifically ones not allowed in valid real numbers. Moreover, the function menu is not active. Let's take a closer look.
Cell class
Individual cells may assume, at any one time, one of three classes: Numeric, Label and Formula. By default, all cells are of class Numeric. You may change the class of a cell at any time by either dropping down the Format menu and clicking on the desired class or simply by pressing the corresponding function key, listed to the right of the menu items. Be aware that invoking this operation clears any data the cell may contain, even if you didn't actually change class.
Numbers may be expressed in scientific notation using the familiar "E" notation, such that 1 × 10 ⋀ 2 is written as 1E2. To cut down on errors, you are allowed to enter only valid characters while in Numeric cells; Opus will alert you should you enter a number in improper format, i.e, 10 – 2. The range for numbers is +/-1 × 10 ⋀ +/- 38 or thereabouts, and the precision is 11 digits.
Of course, Labels and Formulas allow you freedom to enter whatever you desire; the maximum length is 60 characters. When editing Labels and Formulas, you may select a function from the function menu by clicking on the desired category. A menu will drop down, and you should continue pressing the button as you position the mouse over the desired item; to select the item, simply release the button, and the function name will appear in the edit area.
Formatting cells
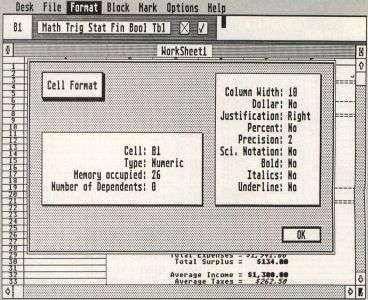
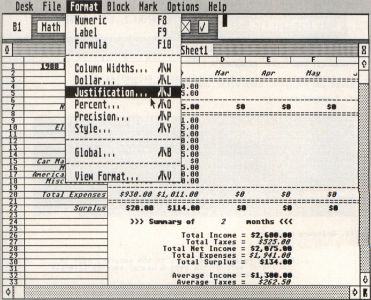
In addition to specifying the class of a cell, you may also control certain parameters affecting the appearance of a cell onscreen and as printed. These parameters or attributes include—in the order listed under the Format menu—Column Width, Dollar, Justification, Percent, Precision and Style. Select one of these from that menu or press the corresponding keyboard-equivalent (the Atari logo means Alternate) and examine the admittedly busy dialog box that appears.
All of these attributes are represented by buttons, and the one you selected is highlighted. The current settings of all attributes for the active cell are displayed, and you may change any combination of these you wish, provided you click on the attribute button(s) before clicking OK. The objects at the bottom of the dialog box allow you to designate the "extent" of the operation; with no block selected and as long as Global was not selected, the active cell will be the default.
Note: You may type in a range in the "Begin" and "End" fields and select the Range button to modify a range of cells or select Global to change the default cell format (and modify all assigned cells). If a block was selected prior to invoking the dialog, the range will appear and the extent will be for that range by default (this applies for all Opus dialogs with range arguments). Note also that you may always override the default extent and attribute selection.
The default class is Numeric, as mentioned earlier; the default format is Column Width = 10, Precision = 2, and Justification = Right for Numerics and Formulas, while Justification = Left for Labels. Experiment with all the formatting features, and you will quickly find ways to emphasize key cells and generally improve your worksheet's appearance.
You may be wondering why I failed to include the option to change cell class in this dialog. Partly it was lack of room, but the main reason is that changing the cell class is a destructive operation, while altering the cell format information leaves the data intact. Later, I'll discuss an easy way to change the class of a range of cells.
Memory considerations
In order to allow for the 254,745 cells making up the Opus spreadsheet, I employed a ";sparse matrix design"; in other words, none of the cells really "exist" prior to containing data. Format and class, among other things, require a cell to exist in order to differ from the default, and a cell which exists consumes memory. The most important consequence is that although you may change the global format at any time, you may not change format over an arbitrarily large range containing many nonexistent cells, because Opus may run out of memory as it creates these cells. Should this occur, it will inform you with a friendly message.
Memory usage information may be found by dropping down the Options menu and clicking on Statistics. Very briefly, unassigned cells of default format consume no memory, Numerics require 26 bytes each, and Labels and Formulas require 88 bytes each. In a stock 512K 520ST with no accessories or resident programs, about 150K is available for the worksheet data, allowing for greater than 5,700 Numerics and about 1,700 Labels/Formulas. Likewise, a one megabyte ST supports more than 24,000 Numerics and about 7,000 Labels/Formulas.
To determine the maximum number of cells for any memory configuration, simply take the value for free memory given by Statistics and divide by 26 or 88, depending on the class you are interested in. I will describe the cell data structure and further discuss memory allocation/deallocation later.
Blocks
Blocks or ranges are simply rectangular groups of cells used by various worksheet operations and also as parameters for certain functions. To define a block, move the cell-cursor to the cell you wish to be the upper-left corner of the block, drop down the Block menu, and click on Start Block (or press the keyboard equivalent, Alt-A); then move the cursor to the cell you want to be the lower-right corner of the block and mark it as the end of the block. You may also select a block by dragging the mouse through a range of cells. Note, however, that this limits you to the cells currently displayed. Finally, you may select an entire row or column as a block by clicking on the row or column title.
Once a block is selected, the cells within the block are displayed in reverse video, and certain menu items are affected. Under the Block menu, Copy, Move, and Delete Block are now available, and under the Mark menu, the items which previously were Show First and Show Last Cell have now become Show Block Start and Show Block End. A list of operations accepting or requiring block information follows.
Auto cursor
To demonstrate this function, drop down the Options menu and make sure that Auto Cursor is checked. Next, select a block and position the cell cursor within it. Now, enter some data and press Return or Enter or click on the data entry icon, and note that the cell cursor moves either to the right or down, providing you did not place it in the last cell of the block.

You may specify the "Auto Cursor direction" through the Options menu. This is in general a quite useful feature and is especially appreciated when a large amount of tabular numeric information is to be entered, as you may first specify the range and then enter the data solely through the numeric keypad, using the Enter key, thus speeding data entry.
Copy, move and delete block
Copy and Move Block are similar commands, differing in that Copy leaves the source block intact, while Move deletes it. For both operations, you first select the source block and then move the cell cursor to the cell you desire to be the start of the destination block. After selecting the command, you are prompted for confirmation, and then you are asked if the operation is to treat cell references within formulas as relative or as absolute.
If absolute is chosen, formulas are copied or moved without change, whereas if relative is chosen, cell references will be adjusted to reflect their new position within the worksheet. Note that if you move the range referenced by a function and not the cell containing the function, the function will not be adjusted to reflect the new position of the range; rather, it will continue to reference the original position. That is, moving the range A1:B2 will not cause any change in a cell outside that block containing the function SUM(A1:B2).
Deleting a block, of course, destroys any data and format information of existing cells within the block. It also frees the memory occupied by those cells as it deallocates them, except if a cell has entries in its "dependent cell list," i.e., if the cell is referenced by a formula in a cell outside the block. Use of the delete icon is equivalent to performing a block-delete on a one-cell block. Note the difference (and reason d'etre) between this icon and the class change function: the latter never deallocates the cell. I'll elaborate on the dependent cell list concept shortly.
More on absolute vs. relative cell references
As mentioned earlier, you may be given the option to consider cell references in formulas as absolute or relative. You may make any cell reference absolute by preceding the row or column by the dollar sign. Examples are: $A1, A$l and $A$1. The dollar sign ensures that, even if Relative was chosen, these cell references (or portions of the reference) will never be adjusted. Of course, this notation has no effect on formula calculation.
Insert and delete rows and columns
These functions appear under the Block menu with their function key equivalents. They define a "virtual block" appropriate for the desired action and perform a block move. After selecting one of these commands, you will be asked to confirm it, specify relative vs. absolute (as above) and also the "sense" of the operation, whole vs. partial. If whole is selected, then the operation will act on the entire row or column containing the active cell.
However, if partial was selected, one of two things may happen. If no block is selected, then a virtual block is assumed beginning at the active cell and extending to the worksheet borders. If a block is selected, a virtual block is defined beginning at the start of the actual block and extending to the border of the worksheet in the direction of the operation and confined to the extent of the actual block in the converse direction.
For example, the range C3:D4 is selected, and you choose to insert a partial row. A row is inserted beginning at row 3 and confined to the columns C and D; the rest of the worksheet is unaffected. If instead you chose Delete Column, a column beginning at column C and confined to rows 3 and 4 is deleted.
Note that Insert causes data in the last row or column to be lost as it moves the virtual block down or to the right. On the other hand, Delete erases the data in the first row or column of the virtual block, as it moves the block up or to the left.
Data fill
This function requests a starting value, an increment and direction (down or right), as well as block coordinates. The increment must always be numeric; however, the starting value may be a number, a weekday name or a month name.
For example, if you were creating a template for a yearly budget organized by months, you could use this function with a starting value of Jan, an increment of 1 and the range A1:A12, and the range would be filled with the abbreviations of all the months of the year, in order. Painless and commonly needed.
You have full control of capitalization and abbreviation, as follows. To capitalize the entire day or month name, make sure at least the first two characters are capitalized to capitalize just the first letter, only capitalize the first letter; and to display in lower case, capitalize no letters. To abbreviate, simply enter the first three characters of the day or month name; otherwise, enter the entire name. Cells of class Label will be created, and they will be left-justified.
Replicate cell
This powerful function allows you to copy a single cell through a range You may again choose relative vs. absolute, but this is really important only for formulas. Replicate greatly facilitates creation of tables where the same formula must be copied through many cells and cell references maintained in a consistent relative fashion.
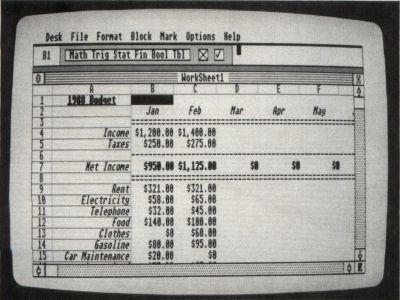
For example, in a budget spreadsheet, you would want to have a cell containing the sum of the expenses. Suppose the expenses, on a monthly basis, were to appear in the ranges A1:A5, B1:B5, C1:C5, and so on, up to L1:L5 for 12 months. These will be simple numerics. The sums would appear in cells A10, BIO, CIO, etc., and the formula in cell A10 would be SUM(A1:A5).
Now, you could enter the remaining formulas by hand, but it is much easier to enter the first one, select the range B10:L10, place the cursor in A10, and replicate this formula through the range. BIO will then contain SUM(B1:B5), CIO will contain SUM(C1:C5), and so on. You may also use this function to copy a cell class with format information through a range.
Again, as in all Opus dialogs requiring cell or range parameters, you may override the default parameters supplied or type in the range rather than first selecting it.
Sort
Sort operates on either a row or column basis within the boundaries of the designated block. It requires a "key cell," which must lie within the block boundaries, and it uses this cell as a compare value against the other cells in its row or column, depending on the direction of the sort. You may also specify ascending vs. descending order, i.e., lowest to highest and vice versa. Precedence is as follows, from lowest to highest:
- Empty Cells that exist
- Numerics = Formulas
- Labels
- 2. Assigned cells (as in 1).
Sorting thoroughly scrambles the cells, so adjusting relative cell references within formulas would almost always be meaningless; thus, it is not done (you probably shouldn't be sorting formulas anyway). For the sake of a printout, you may occasionally need to sort formulas, and you may wish to first save the worksheet to preserve the relationships.
Alternatively, you might fill a range using Data Fill such that the first formula has a corresponding number 1, the second 2, etc. These numbers will then "follow" the formulas to their new location, and you may restore the original order simply by sorting the range in ascending order using any cell within this "number field" as the key cell.
Formulas
Opus provides more than 40 functions for use in formulas. A comprehensive list is found under the Help menu, and I will describe them more fully here. But first, some general considerations.
Formula Entry. To enter a formula, you must first change the cell class to Formula by either dropping down the Format menu and clicking on Formula or pressing F10. Then, you may enter any valid algebraic expression, using cell references and any combination of supported functions. Remember, cell references can be made by "shift-clicking" on a displayed cell, and all functions may be entered using the function menu.
Recalculating. Opus provides "natural order" recalculation; that is, instead of just "grabbing" the current value of a cell reference to a formula, Opus will first recalculate the formula. Thus, formulas are evaluated using up-to-date values, independent of position within the worksheet. This ensures accuracy and reliability.
Opus also provides automatic recalculation, so that a change in one cell causes all cells containing formulas that reference the changed cell to be recalculated, while all other cells will not be affected. This feature increases speed of recalculation, as you may change the value of one cell and immediately see the results in affected cells, without having to wait for all other cells to be recalculated.
Both automatic recalculation and natural order are defeatable through the Options menu, and turning them off may speed global recalculation of large spreadsheets somewhat. I'll discuss another reason to disable these features later, but for the vast majority of cases, you should just leave them on.
In order for Opus to provide automatic recalculation, cells referenced by formulas must exist, for these cells need to "know" they are referenced and who their "dependents" are so that Opus knows which cells to reevaluate when the value of a cell changes. Thus, if a referenced cell does not exist, it will be created, consuming 34 bytes of memory (the standard 26 bytes plus eight bytes to indicate its dependent). Essentially, every non-redundant cell reference creates an entry in the referenced cell's "dependent-cell list," and each of these entries requires eight bytes. Information on the total number of dependents is found through Options/Statistics.
One problem with natural order and automatic recalculation is the handling of "circular" cell references. For example, cell A1 contains the formula B1*2 and B1 contains the formula A1*2. Were natural order calculation in effect, the expression evaluator would try to recalculate B1 before using its value for the formula in A1. But, it would then see that B1 depends on A1, so it would try to recalculate A1, but since A1 depends on B1, it would need to recalculate B1, and so on. If this infinite looping was allowed to go unchecked, the machine's stack would be overrun, leading to a crash.
The solution to this is simple: set a bit in the format field of the cell when it is recalculated, but its result is "pending," and test this bit before attempting to recalculate it. It is also necessary to use another bit to indicate "completed recalculation." The net effect is this: if a cell reference refers to a pending cell, then the cell containing the formula can't be recalculated at that time, so we jump to the end of the procedure and continue.
Generally, the cell will later be fully evaluated in the course of a global recalculation or provided another cell references it. Since evaluation stops at that point, syntax errors in the formula occuring after the pertinent cell reference can slip by.
As can be inferred from the above, I consider circular references to be errors and only support them in the sense that the machine definitely will not crash should it encounter one. I make no guarantees regarding the accuracy or predictability of their results, so please, take care not to use them.
Now let's consider the actual formula building blocks: values, operators, and functions.
Values. Values are comprised of real numbers and cell references; the formats of each have been previously described. However, in the formula context (but not in Numeric cells), you may append a number with the percent sign, and the expression evaluator will divide the number by 100 before using it. This doesn't work for cell references, since you may specify cell format as percent and achieve the same result. Opus doesn't allow string data in formulas. Consequently, for the purpose of recalculation, Opus considers Labels to have values of zero or one (whatever is appropriate), ignoring the string it may contain.
Operators. Opus provides the standard arithmetic operators, listed below in order of precedence, from highest to lowest, with operators of equal precedence listed on the same line:
- (negation)
⋀ (exponentiation)
* /
+ -
= < >< = > = <> (logical perators)
Parentheses may be used in the standard fashion to group operations and force calculation to proceed in the desired order, and expressions may be arbitrarily complex.
Functions. The general function format is "function name" (argument list). For discussion's sake, I'll consider related functions together in groups or "libraries," as they are listed in the Function menu and in the Functions selection of the Help menu. (For programming purposes, they are arranged in libraries on the basis of the number or types of arguments they require.)
Ranges are written "cell reference : cell reference." An example is SUM(A1:G1O). Note that when a range is used by a function, every cell in that range will have its dependent cell list updated to contain a reference to the cell holding the formula, and if any of these cells do not exist, they will be allocated if memory allows. Therefore, one can not reference an arbitrarily large range in a function.
The math functions supported by Opus are:
- LN(x), EXP(x): Natural logarithm (Base e) and antilogarithm.
- LOG(x): Base 10 logarithm (to get Base 10 antilog, 10⋀x).
- SQR(x), SQRT(x): Square of x and square root of x.
- DIV(x,y): Divides x by y and returns integer portion of quotient.
- MOD(x,y): Returns the remainder of x divided by y. Both MOD and DIV are real-valued functions and are related by the equation x = DIV(x,y)*y+ MOD(x,y).
- ABS(x): Returns the absolute value of x.
- ROUND(x.y): Rounds the number x to y places. If y is zero or negative, then the integer portion of x is rounded. Ex., ROUND(567.89,1) returns 567.9; ROUND(567.89, — 1) returns 570.
- TRUNC(x,y): Truncates the number x to y places; y acts as in ROUND. Equivalent to INT in other spreadsheets when y = 0.
- RAND(x,y): Returns a random number n such that x < n < y.
- FAC(x): Returns the factorial of x; 0 < = x < = 33.
The trigonometric functions supported by Opus are:
- SIN(x), COS(x), TAN(x): These all expect the angle to be in radian units, i.e., radians = degrees X (pi/180).
- ASIN(x), ACOS(x), ATAN(x): Inverses of the above. Again, they return the angle in radians.
- RAD(x): Converts angle in degrees to radians.
- DEG(x): Converts angle in radians to degrees.
- PI(): Returns the value pi (the parentheses are necessary!).
The statistical functions supported by Opus are:
1. SUM(range), PROD(range), MAX(range), MIN(range), COUNT (range):
SUM adds all values within the range. Labels and unassigned cells are considered to equal zero.
PROD returns the product of all cells within the range. Labels and unassigned cells are considered to equal one.
MAX and MIN return the maximum and minimum values within the range. Labels and unassigned cells are not considered.
COUNT returns the number of cells within the range containing numeric values, including formulas. Labels and unassigned cells aren't counted.
2. MEAN(range), VAR(range), SDEV(range), SERR(range):
MEAN returns the average of all cells containing numbers. Labels and unassigned cells are not considered.
VAR returns the sample variance of numeric values within the range.
SDEV returns the sample standard deviation of the values within the range.
SERR returns the sample standard error (standard deviation of the mean) of the values within the range.
3. LINR(y-range,x-range), CORR(y-range.x-range), REDV(y-range,x-range,x):
LINR: Linear regression via the least squares method returns the slope of the regression line in the cell containing the formula and the y-intercept in the cell immediately to its right. The "y range," of course, refers to the dependent variable (ordinate) and "x range" to the independent variable (abscissa). The ranges may extend over some unassigned cells, but a one-to-one correspondence between the two variable lists must exist. Also, one range may be horizontal and the other vertical, and either may extend over more than one row or column, i.e., A1:B5. If A1:B5 was the y-range, then for the sake of relating y to x, value 1 would be cell Al, value 2 Bl, value 3 A2, and so on; the evaluator proceeds by rows or in "row-major order" in such cases.
CORR: Parameters are the same as in LINR. This function calculates the correlation coefficient for the linear regression. This value is a measure of the goodness of fit of the regression line and always falls between —1 and 1, such that CORR approaches 1 as the data approximates more and more closely a linear relationship. CORR approaches —1 as the data approximates a negative linear relationship, i.e., a straight line with a negative slope. CORR approaches zero for data that is not linearly related.
PREDV: Parameters are similar to LINR and CORR, except this function expects an additional parameter, x. PREDV returns the predicted value of the dependent variable using the slope and intercept derived from linear regression on the data set, i.e., it returns y from y = mx + b. The usefulness of CORR is apparent in the context of this function; the closer CORR is to 1 or —1, the more "believable" the PREDV. Note that use of this function is most suited for x = values lying within the range defined by the minimum and maximum values of the x-range; results based on values lying outside this range may or may not be valid.
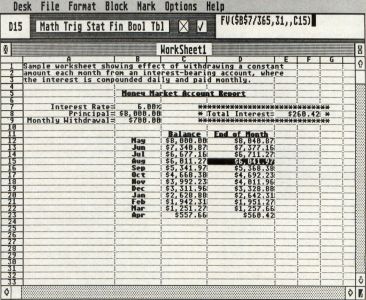
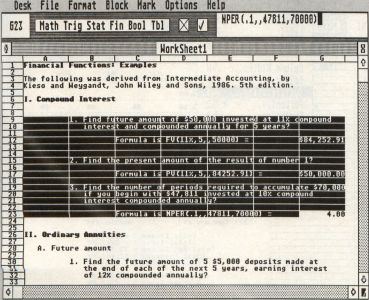
The financial functions supported by Opus are:
PV(rate, # periods, payment, future value, "type")
FV(rate,#periods, payment, present value, "type")
NPER(rate, payment, present value, future value, "type")
PMT(rate, #periods, present value, future value, "type")
For all of these functions, the "type" argument is optional; it allows you to specify for annuity calculations whether the calculation is for an ordinary annuity (type = 1) or an annuity due (type = 0). An ordinary annuity is the default for annuity calculations (payments occur at end of periods). It is up to you to provide correct rate and # periods arguments.
PV: Calculates the present value of an annuity or single sum, based on compound interest for the latter. For a single sum, leave out the payment argument, and insert a comma in its place instead. For an annuity calculation, leave out the future value argument and only insert a comma in its place if you include the type argument.
FV: Calculates the future value of an annuity or single sum; usage is similar to PV.
NPER: Calculates the number of periods for an annuity or the number of periods required to reach a given future value from a given present value in a compound interest calculation. Again, usecommas as place-holders to skip arguments if necessary.
PMT: Calculates the payment or rent for annuities. Present and future value arguments may not be present simultaneously.
Obviously, these commands are powerful and very flexible, and they can be somewhat confusing as a result. Various combinations of arguments are possible, and some are not permitted. For example, specifying the type argument for a compound interest calculation FV(10%, 5,,100) would be illegal. Unfortunately, lack of space precludes detailed discussion on usage and principles of these financial functions; however, any good accounting or business math book would be suitable as a reference and will provide examples for you to solve using these functions.
The Boolean or logical functions supported are:
The logical operators have already been listed; they may be used at any time but are most useful when used in conjunction with these functions. An example "condition" as intended below is Al = 1; however, it may be any valid expression.
- IF(condition,action,alternate action): When "condition" evaluates to a non-zero number (TRUE), "action" is performed, and if condition evaluates to the number zero (FALSE), the "alternate" action is taken. The condition is most commonly a comparison between a cell and a value or two cells but may be any valid expression or even just a number. The two actions may themselves be any valid expression, including IFs, so that IF-THENIF-THENELSE type constructs may be used. As an example:
IF(A1 = 2,IF(A2 > 3,l,0),A4) reads: IF Al = 2 THEN IF A2 > 3 THEN return 1 ELSE return 0 ELSE return the value of A4. - AND (condition, condition, condition . . .): Independently evaluates all conditions and returns one (TRUE) if all conditions returned non-zero values and zero (FALSE) if any of the conditions returned zero. Between two and twenty conditions may be supplied (this applies to OR as well). Of course, this may be used in IFs, and IFs can serve as conditions.
- OR (condition, condition, condition . . .): Similar to AND, except OR returns one if any of the conditions returned non-zero values and zero only if all equalled zero.
- NOT(condition): Returns one if condition evaluates to zero, and returns zero if condition evaluates to a non-zero value.
The Table LookUp functions provided in Opus are:
- INDEX(row index, column index, range)
- VLOOKUP(value, index, range)
- HLOOKUP(value, index, range)
These three functions allow you to create tables of data and then extract information in a predictable way. They are very useful for such things as tax tables or grade assignments.
INDEX: This function adds the row and column numbers you provide to the coordinates of the first cell in the range and returns the value of the cell at the resulting coordinates. For example, INDEX(2,3,A1:C5) returns the value of cell C2, that is the cell found at the second row and third column within the range. Likewise, INDEX(1,1,A1:C5) references the first cell, Al. The row and column indices may be expressions; it is an error to reference a cell outside the range.
VLOOKUP: This function searches in the first column of the indicated range for the greatest value less than or equal to the value you supplied, and it returns the value in the same row but in the column equal to the first column plus the index. The function is a "vertical lookup," as it searches in the vertical direction. An error occurs if no match is found or the index references a location outside the block. As an example, consider a grading scale where 0-59 is an F, equal to zero quality points, 60-69 is a D, equal to one quality point, 70-79 is a C, 80-89 is a B and 90 and above is an A. We can construct a lookup table to assign these quality points as shown in Table 1.
| A | B | C | D | |
| 1 | Score | Points | Scale | Quality Points |
| 2 | 75 | 2 | 0 | 0 |
| 3 | 88 | 3 | 60 | 1 |
| 4 | 70 | 2 | 70 | 2 |
| 5 | 93 | 4 | 80 | 3 |
| 6 | 59 | 0 | 90 | 4 | Table 1 |
The basic formula to access the table and assign the point values is entered in cell B2 as VLOOKUP(A2,2,$C$2:$D$6). This formula is then replicated through the range B2:B6 to complete the table, using the relative option.
HLOOKUP: Complementary to VLOOKUP, this function searches the first row of the indicated range. Thus, it is an "horizontal lookup" function. Using Table 2 as an example, HLOOKUP(2.5, 3,A1:D3) returns 4 (value of B3); HLOOKUP(1,4,A1:D3) returns an error, as the index referenced a location outside the range.
| A | B | C | D | |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2.3 | 3 | 5 | 8 |
| 3 | 7.8 | 4 | 7 | 16 |
| Table 2 |
In order to function properly, both VLOOKUP and HLOOKUP expect the lookup column or row, respectively, to be sorted in ascending order. If it is not, an error message may result, or the function may simply return an incorrect value.
Caveats
I had earlier purported that Opus provides "comprehensive" error-trapping, and in general, this is not an unfounded claim. Division by zero, attempting square roots of negative numbers, attempting logarithms of numbers less than or equal to zero, raising a number to too great a power, etc., are trapped and flagged as errors, since it is a reasonably simple matter to do so.
Unfortunately, the standard Personal Pascal response to a floating point overflow is a system crash, and I was unable to obtain information necessary to alter this. Thus, short of writing my own assembly language floating point routines, there is nothing within reason I can do to prevent a crash if you enter a formula such as 1E2O*1E2O. This also applies to functions such as LINR and SDEV, which perform multiplications and divisions "hidden" to the user, but this should be an exceedingly rare problem unless you are commonly performing these operations on numbers near the real number bounds.
Error messages
Every existing cell has a "status" field, which indicates if it is empty, assigned, or has an error condition associated with, in which case a small message will be displayed in the cell. The error messages are "Division by Zero," "Overflow," "Undefined," "Bad Real Number," "Bad Cell Reference," "Out of Range," "Syntax Error," and a "Generic Error." If evaluation of a newly entered formula results in an error, a dialog box will appear, and you may immediately correct any mistake if you so desire. If not, the formula will be stored as entered, and the cell will assume the error status.
Formulas that reference a cell with an error status will themselves assume the same error status upon calculation. Of course, once a cell with error status assumes a non-error status, the display will be updated to reflect the changes.
Files
Opus is capable of producing two types of files: loadable worksheet files identified by the filename extender "OPS" and ASCII files with the extender "DOC" suitable for printing from the desktop or loading into word processors. The latter is equivalent to printing to disk, except that no printer control codes are stored.
You may choose to save the entire worksheet or just a block. When loading a block, you are given the option to load at the original location within the sheet or at the cursor location. If the latter is chosen, cell references are adjusted as if the block had been moved from its original location.
When saving a worksheet, information is stored only for allocated cells (naturally). Further, since we needn't store on disk such things as the values of pointers and contents of dependent cell lists, worksheet files always consume less space than do their in-memory counterparts. And, although Personal Pascal doesn't provide variable length strings (which requires us to declare all strings as maximum length), we can fairly easily save just the actual string length for labels and formulas, yielding a great reduction in required disk space.
Various worksheet parameters are saved for both blocks and sheets. These include the column widths, status of the "checkable" menu items under the Options menu, the titles, headers, etc. of the Print/Save as Text dialog, and the default cell format. When loading a block, these worksheet settings will not be altered, the rationale being that you will build a library of commonly needed formulas for later incorporation into sheets; however, you may elect to load a block "as a sheet," and the settings in this case will be altered to reflect those of the file.
Another important difference in loading sheets vs. blocks is that the former clears the worksheet, while the latter does not. Loading a block "as a block" is thus equivalent to a merge.
Opus's file structure is proprietary (my euphemism for incompatible with everything), meaning that it can only read files it created. Conversely, other programs won't be able to use Opus files. As a positive aspect, Opus files tend to be somewhat smaller than other spreadsheet programs'.
Printing
As mentioned earlier, Opus is supplied with an EPSON-compatible printer driver, called PRINTER.INF. It must reside in the same directory as OPUS.PRG and OPUS(M/H).RSC. INSTALL.PRG allows you to create drivers for other printers. See the printer manual for control codes, and follow the instructions in the dialog, as INSTALLS error-trapping is somewhat less than extensive!
Opus supports multiple features providing attractive onscreen formatting, including individual cell justification and text special effects. These are not lost upon printing, so that you get "what you see is what you get" or WYSIWYG (wiz-i-wig) output.
Drop down the File menu and click on Print. Examine the dialog box that appears. You may enter two (or none) title lines of up to 40 characters each, and these will appear, centered, on the first page of the printout. You may enter a one-line each header and footer, which appear on every page. You should check the Help menu item for description of the control codes allowed in headers and footers, which allow justification, inclusion of date/time, filename and page number.

You may also specify whether the output is to be at regular pitch or condensed; you may choose to make "condensed" the 96 char/line mode rather than 137 char/line; just be sure to update PRINTER.INF via INSTALL, including the "Condensed Char/Line" field as well as the printer control code field.
If you check "Show Formulas," formulas will be printed out in source form rather than as values, which is handy for documenting and debugging your spreadsheets. You may choose to suppress the row numbers and column letters for final reports. Last, you may control draft vs. near letter quality print providing your printer supports this option.

Printing (and saving as text) requires that you specify a block, and the default block is the smallest one encompassing all defined cells. So you need do nothing to print the entire worksheet, unless a block is selected, in which case that block will be the default. The print algorithm fits as many cells per line as are possible, given the number of print columns as per PRINTER.INF. It then prints as many of those lines as will fit on a page, which is always 66 lines long.
It continues to print those columns until all indicated rows have been printed. Then it moves on to the adjacent columns, if any, and it repeats itself in this manner until done. A dialog appears while printing and shows the current page number, and you may cancel the print at any time by pressing Escape.
Potpourri
Opus supports dual windows, suppression of grid lines, and several other options; review the menu items and experiment! Options/Clear Worksheet offers a choice of "clear mode." When "Number" is chosen, only cells with Numeric class are cleared. This is handy for spreadsheets that are used again and again as templates, as it preserves the formulas and labels and erases only the numeric data.
Options/Freeze Titles allows you to "lock" a row or column or both on screen, so that you may not scroll past it. Further, the locked row/column remains on screen as you scroll away from it. This is very useful for data entry over large ranges, as you may keep your labels on screen at all times. This has no effect on printing.
The Mark menu facilitates moving about the spreadsheet; you may directly go to any cell via Goto Cell, go to the start/end of the worksheet/block, and go to a "marked" cell via Set/Goto Mark.
Stay tuned
You should now have all the information you need to get the most out of Opus. For the programmers among you, a discussion of the programming techniques involved in writing a spreadsheet program will be presented in next month's ST-Log. Be there!