IBM Fractal Graphics
Paul W. Carlson
One of the hottest topics in mathematics these days is fractals—fractional dimensions. Fractals are being used for everything from simulating random plant growth to generating realistic planetary landscapes for science-fiction films and arcade games. This article, adapted from "Apple Fractals" in the September 1985 issue of COMPUTE!, introduces the fascinating world of fractals with three programs that work on any IBM PCjr or PC with color/graphics adapter.
The term fractal was coined by Benoit Mandelbrot, a pioneer in their study, to denote curves or surfaces having fractional dimension. The concept of fractional dimension can be illustrated as follows: A straight curve (a line) is one-dimensional, having only length. However, if the curve is infinitely long and curves about in such a manner as to completely fill an area of the plane containing it, the curve could be considered two-dimensional. A curve partially filling an area would have a fractional dimension between one and two.
Many types of fractals are self-similar, which means that all portions of the fractal resemble each other. Self-similarity occurs whenever the whole is an expansion of some basic building block. In the language of fractals, this basic building block is called the generator. The generator in the accompanying programs consists of a number of connected line segments. The curves that the programs plot are the result of starting with the generator and then repeatedly replacing each line segment with the whole generator according to a defined rule. Theoretically, these replacement cycles would continue indefinitely. In practice, the screen resolution limits the number of cycles.
The programs illustrate two types of fractal curves. The curves generated by Program 1 and Program 2 are self-contacting, while the curve generated by Program 3 is self-avoiding. A self-contacting curve touches itself but does not cross itself. A self-avoiding curve never actually touches itself although it may appear to because of the limited screen resolution.

The Dragon Sweep
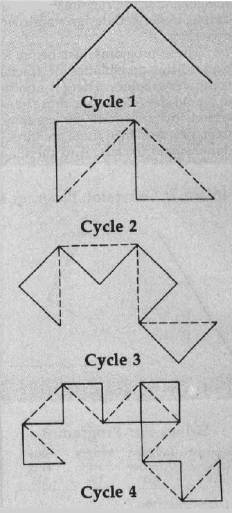
Program 1 plots what Mandelbrot refers to as a "dragon sweep." It demonstrates in a step-by-step fashion how a fractal curve is filled. The generator consists of two line segments of equal length forming a right angle. During each replacement cycle, the generator is substituted for each segment on alternating sides of the segments, that is, to the left of the first segment, to the right of the second segment, and so on. Figure 1 shows the first few cycles of substitution. The program is written in BASIC so the plotting is slow enough to let you observe the development of the curve.
The program prompts you to enter an even number of cycles (for reasons of efficiency and screen resolution, only even numbers of cycles are plotted). When a plot is complete, pressing any key clears the screen and returns you to the prompt. I recommend starting with two cycles, then four, six, etc. It takes fourteen cycles to completely fill in the "dragon," but since this requires almost two hours, you will probably want to quit after about ten cycles. You can see the complete dragon by running Program 2, which always plots the dragon first in less than 30 seconds.
Since it's not at all obvious how the program works, here's a brief explanation. NC is the number of cycles; C is the cycle number; SN is an array of segment numbers indexed by cycle number; L is the segment length; D is the segment direction, numbered clockwise from the positive x direction; and X and Y are the high-resolution screen coordinates.
| Line 100-140 | Get number of cycles from user. |
| Line 150 | Computes segment length. |
| Line 160 | Sets starting coordinates. |
| Line 170 | Sets segment numbers for all cycles to the first segment. |
| Line 180-220 | Find the direction of the segment in the last cycle by rotating the segment in each cycle that will contain the segment in the last cycle. |
| Lines 230-260 | Increase or decrease X or Y by the segment length, depending on the segment direction. |
| Lines 270-290 | Plot the segment and update the current segment number for each cycle. |
| Lines 300-320 | If the segment number for cycle zero is still zero, do the next segment; otherwise, we're done. |

Eight Thousand Dragons
Program 2 plots more than 8,000 different dragons. It does this by randomly determining on which side of the first segment the generator will be substituted for all cycles after the first cycle. The generator is always substituted to the left of the first segment in the first cycle to avoid plotting off the screen. Other than the randomization, this program uses the same logic as Program 1. The main part of this program is written in machine language to reduce the time required to plot a completely filled-in dragon from about two hours to less than half a minute.
All the dragons are plotted after 14 cycles of substitution. All have exactly the same area, which equals half of the square of the distance between the first and last points plotted. All the dragons begin and end at the same points.
When a plot is complete, press the space bar to plot another dragon, or press the Q key to quit.

Snowflakes
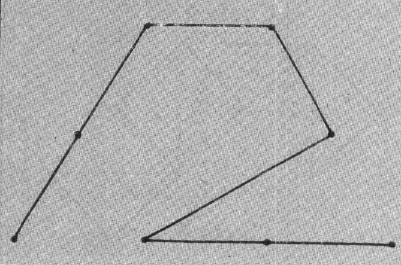
Program 3 plots what Mandelbrot refers to as a "snowflake sweep." The generator, shown in Figure 2, was discovered by Mandelbrot. The segments are numbered zero through six, starting at the right. The program is basically the same as Program 1. The variables NC, C, SN, D, X, and Y represent the same values except that the direction D is numbered counterclockwise from the negative x direction. For each segment, the accompanying table gives the value of RD (relative direction), LN (length factor), and SD (flags indicating which side of the segment the generator is to be placed).
| Line 20 | Reads values of SD and RD. Compute LN values. |
| Lines 30-50 | Compute delta x and delta y factors for each direction. |
| Lines 60-100 | Get number of cycles from user. |
| Lines 120 | Sets starting coordinates. |
| Lines 130 | Sets the segment numbers for all cycles to the first segment. |
| Lines 140-170 | Find the direction of the segment in the last cycle. |
| Lines 180-190 | Compute the coordinates of the end of the segment, plot the segment, and update the segment numbers for each cycle. |
| Lines 200-220 | Same as lines 300-320 in Program 1. |
Like Program 1, pressing any key when a plot is complete clears the screen and brings another prompt.
Experiment
I hope these programs encourage you to look further into the fascinating world of fractals. Don't be afraid to experiment with the programs-try modifying the shape of the generator in Program 3, for example. Better yet, design your own generator.
These programs just begin to explore the possibilities of fractal computer graphics. There is another whole class of fractals, those generated by functions of complex variables. And then there are three-dimensional fractals. And then …
| Values For Program 3 | |||
| Segment Number SN | Relative Direction RD | Length Factor LN | Side Flag SD |
| 0 | 0 | 1/3 | 0 |
| 1 | 0 | 1/3 | 1 |
| 2 | 7 | √1/3 | 1 |
| 3 | 10 | 1/3 | 0 |
| 4 | 0 | 1/3 | 0 |
| 5 | 2 | 1/3 | 0 |
| 6 | 2 | 1/3 | 1 |
Program 1: The Dragon Sweep
MH 90 DIM SN(14):KEY OFF MN 100 CLS:SCREEN 0 PI 110 PRINT "ENTER AN EVEN NO. 0 F CYCLES (2 TO 14)" DD 120 INPUT"OR ENTER A ZERO TO QUIT: ";NC EH 130 IF NC = 0 THEN KEY ON: END MO 140 IF NC MOD 2 = 1 OR NC < 2 OR NC > 14 THEN 100 DL 150 L = 128: FOR C=2 TO NC STEP 2:L-L/2:NEXT AE 160 X = 192:Y=133:CLS:SCREEN 2: PSET <X,Y),1 DL 170 FOR C = 0 TO NC:SN(C)=0:NEXT K KJ 180 D=0:FOR C=l TO NC: IF SN(C-1)=SN(C) THEN D=D-l:GOTO 200 GC 190 D=D+1 BP 200 IF D=-l THEN D=7 MI 210 IF D=8 THEN D=0 NC 220 NEXT OA 230 IF D=0 THEN X=X+L+L:GOTO 270 EH 240 IF D=2 THEN Y=Y+L:GOTO 270 GA 250 IF D=4 THEN X=X-L-L: GOTO 270 GM 260 Y=Y-L PL 270 LINE -(X,Y),1:SN(NC)-SN(NC) + 1 QP 280 FOR C=NC TO 1 STEP -1: IF SN(C)<>2 THEN 300 OH 290 SN(C)=0:SN(C-1)=SN(C-1)+1:NEXT GA 300 IF SN(0)=0 THEN 180 MM 310 IF INKEY$="" THEN 310 AC 320 GOTO 100
Program 2: Eight Thousand Dragons
PP 100 DEF SEG: CLEAR, &H3FF0:N=&H4000
LL 110 READ A$: IF A$="/" THEN 130
LI 120 POKE N,VAL("&H" + A$) :N=N + 1: GOTO 110
OC 130 N = &H440F: FOR K=1 TO 15:POKE N,0:N = N + l: NEXT
NH 140 POKE &H4425, 0
IF 150 N=&H4000:CALL N:POKE &H4425, 1
EA 160 A$ = INKEY$:IF A$ = "" THEN 160
PI 170 IF A$=" " THEN 150
ID 180 IF A$<>"Q" AND A$ <>"q" THEN 160
IH 190 SCREEN 0: CLS: KEY ON: END
EI 1000 DATA 1E, 0E, IF, B8, 05, 00, CD, 10, 80, 3E
DN 1010 DATA 25, 44, 00, 75, 0B, B4, 00, CD, 1A, 89
NF 1020 DATA 16, 23, 44, EB, 31, 90, BE, 02, 00, B9
OE 1030 DATA 08, 00, A1, 23, 44, 33, D2, A9, 02, 00
JE 1040 DATA 74, 02, B2, 01, A9, 04, 00, 74, 02, B6
NG 1050 DATA 01, 32, D6, D0, EA, D1, D8, E2, E8, A3
BJ 1060 DATA 23, 44, 24, 01, 88, 84, 0F, 44, 46, 83
FH 1070 DATA FE, 0F, 75, D3, B8, 00, 06, 33, C9, BA
LI 1080 DATA 4F, 18, 32, FF, CD, 10, B9, 0F, 00, 33
NJ 1090 DATA F6, C6, 84, 00, 44, 00, 46, E2, FB, C7
JD 1100 DATA 06, 1E, 44, 60, 00, C7, 06, 20, 44, 84
HF 1110 DATA 00, B8, 01, 0C, 8B, 0E, 1E, 44, 8B, 16
DC 1120 DATA 20, 44, CD, 10, C6, 06, 22, 44, 00, B9
LO 1130 DATA 0E, 00, 33, FF, BE, 01, 00, 8A, A5, 0F
KC 1140 DATA 44, 80, FC, 00, 75, 18, FE, 06, 22, 44
CL 1150 DATA 8A, 85, 00, 44, 3A, 84, 00, 44, 75, 20
LG 1160 DATA FE, 0E, 22, 44, FE, 0E, 22, 44, EB, 16
OD 1170 DATA FE, 0E, 22, 44, 8A, 85, 00, 44, 3A, 84
HK 1180 DATA 00, 44, 75, 08, FE, 06, 22, 44, FE, 06
DC 1190 DATA 22, 44, 80, 3E, 22, 44, FF, 75, 07, C6
HN 1200 DATA 06, 22, 44, 07, EB, 0C, 80, 3E, 22, 44
NN 1210 DATA 08, 75, 05, C6, 06, 22, 44, 00, 47, 46
FE 1220 DATA E2, AB, EB, 02, EB, 9A, 80, 3E, 22, 44
CH 1230 DATA 00, 75, 06, FF, 06, 1E, 44, EB, 1E, 80
KP 1240 DATA 3E, 22, 44, 02, 75, 06, FF, 06, 20, 44
IG 1250 DATA EB, 11, 80, 3E, 22, 44, 04, 75, 06, FF
CO 1260 DATA 0E, 1E, 44, EB, 04, FF, 0E, 20, 44, B8
ID 1270 DATA 01, 0C, 8B, 0E, IE, 44, 8B, 16, 20, 44
LL 1280 DATA CD, 10, FE, 06, 0E, 44, BF, 0D, 00, BE
KL 1290 DATA 0E, 00, B9, 0E, 00, 80, BC, 00, 44, 02
PI 1300 DATA 75, 0D, C6, 84, 00, 44, 00, FE, 85, 00
FM 1310 DATA 44, 4F, 4E, E2, EC, 80, 3E, 00, 44, 00
OK 1320 DATA 75, 02, EB, 9C, 1F, CB,/
Program 3: The Snowflake Sweep
DE 10 DIM DX(11), DY(11):KEY OFF
MC 20 FOR N = 0 TO 6: READ SD(N), RD(N) : LN(N)=1!/3!:NEXT:LN(2) = SQR(LN(l))
LC 30 A = 0: FOR D = 6 TO 11:DX(D) = COS(A):DY(D) = SIN(A)
JN 40 A = A + .52359879#:NEXT
CK 50 FOR D = 0 TO 5:DX(D)= - DX(D + 6):DY(D) = - DY (D + 6):
NEXT:X1 = 5 34:Y1 = 147: TL = 324
OG 60 CLS: SCREEN 0
AB 70 PRINT "ENTER NUMBER OF CYCLES (1 - 4)"
GK 80 INPUT "OR ENTER A ZERO TO QUIT: ";NC
JA 90 IF NC = 0 THEN END
DA 100 IF NC > 4 THEN 60
OP 110 CLS:SCREEN 2
CL 120 X = 534: Y = 147: TL = 324: PSET(X,Y), 1
CD 130 FOR C = 0 TO NC:SN(C) = 0:NEXT
MI 140 D = 0: L = TL: NS = 0: FOR C = 1 TO NC: I = SN(C):
L = L*LN(I):J = SN(C-1):NS = NS + SD(J):IF NS MOD 2 = 1 THEN D=D+12-RD(I):GOTO 160
GE 150 D=D+RD(I)
EG 160 D = D MOD 12
OL 170 NEXT
BN 180 X = X + 1.33*L*DX(D):Y = Y-.5*L*DY(D):LINE -(X, Y), 1:
SN(NC) = SN(NC) + 1: FOR C = NC TO 1 STEP -I: IF SN(C) <> 7 THEN 200
OG 190 SN(C) = 0: SN(C-1) = SN(C-1) + 1: NEXT
AH 200 IF SN(0) = 0 THEN 140
KE 210 IF INKEY$="" THEN 210
PD 220 GOTO 60
AF 230 DATA 0, 0, 1, 0, 1, 7, 0, 10, 0, 0, 0, 2, 1, 2