Adding
Sound Effects
To Atari
Matt Giwer
To Atari
Matt Giwer
Do you want more realistic sounds than beeps? This article gives you five short programs that let your Atari produce some interesting, subtle sounds.
There are many packages available for making the Atari a music box. All provide some degree of musical verisimilitude; that is, they sound good. However, these packages don't really help those who are tired of hearing the same old beeps in their programs.
Let's consider how tones are generated in the real world and try to duplicate them on the computer. And take heart: It will all be done in BASIC. You won't even find a page 6 subroutine. You can improve on what I have done once you understand what is going on.
Frequencies And Amplitude
Sound is generated by vibrating objects. Each object sounds different because it has a different set of resonant frequencies. Also, each object has a different set of loss parameters that determine how quickly the amplitude of the sound will rise and fall. Other factors such as the noise content add to the character of each individual sound.
The resonant frequency of an object is the dominant characteristic, so let's take it first. Strike a bell or play a note on a piano and you don't hear just one frequency, you hear a wide range of frequencies. The lowest frequency is called the fundamental frequency. Most objects also support harmonics of this frequency. The even harmonics are two, four, six, eight, and so forth times as high as the fundamental. The odd harmonics are three, five, seven, nine, and so forth times as high.
The mix of these frequencies and whether they are odd or even are components of the character of the sound. A piano is rich in even harmonics; a woodwind is rich in odd harmonics. There is one further complication: Most objects have more than one fundamental frequency, and each fundamental frequency may have its own set of harmonics. It is thus obvious why simple beeps lack the complexity of real sounds.
The next factor is how fast the amplitude of these frequencies rises and falls. When a drum is struck, it gives a short, loud sound, so its amplitude rises and falls quickly. A piano note is loud, but is sustained for some time. A woodwind rises slowly in amplitude and falls slowly.
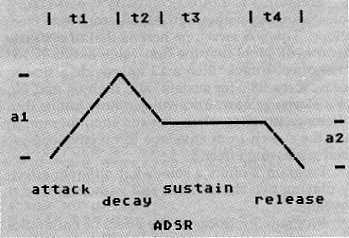
The simplification used for electronic simulation of musical instruments is called the ADSR envelope (shown in the figure). These letters stand for Attack, Decay, Sustain, and Release. Across the top are times 1 through 4 and amplitudes 1 and 2. A struck instrument has a very short t1 and a somewhat longer t2. For a piano, t3 and t4 are relatively long and for a drum, t3 and t4 are short. Also for struck instruments the amplitude al will be at least twice as great as a2, but in a woodwind they may be the same.
Noise And Tone
The third factor is the amount of noise. This is easily heard in a snare drum, which contains added wires to make noise. It is less obvious in woodwinds, where the very act of blowing creates some noise. Blowing is similar to whispering, where there is little tonal content and the lips and tongue are modulating noise. A "breathy" speech pattern is comparable to a horn or woodwind. Thus a low amplitude component of noise can add to the realism.
With these three factors in mind, let's examine a woodwind in detail. The artist is aware that the instrument has a slow attack time, so he will blow harder at the beginning of a note to give it a definite start. In doing so he will increase the noise level. The initial breath will start the instrument vibrating, and the various fundamentals and harmonics will be heard. If the instrument is being played loudly, some of the harder-to-excite frequencies will be heard too.
Once the instrument has established its note, the artist will blow more softly, so the tone content will be up, but the noise component will be down. Finally the note will end, and the artist will stop blowing. The noise component will stop immediately, but the tonal component will continue for a short time. If all this doesn't sound complex enough, imagine what goes on in a slide trombone.
Real sounds are complex, but computergenerated tones are not. So we must make them complex to make them realistic. For a perfect simulation of a piano or clarinet, a Moog synthesizer is definitely preferred. To make do with the Atari sound chip, machine language might be preferable. But if you draw a line with one end being the beeps and the other end the Moog, we'll see that BASIC can get us more than halfway toward the Moog.
Experimenting With Sound Qualities
The following programs are examples of some complex sonic effects. These programs directly POKE the audio control registers with amplitude information. The amplitude varies from 0 (off) to 15 (loudest). These amplitude levels are stored in S0$ in pairs of numbers. These are converted to numbers in line 21 and POKEd in line 22. The cycle through the loop provides automatic timing for note duration. Q=1 ^ 1 is used for timing pure tones.
Program 1 is a direct comparison between notes with and without an ADSR amplitude envelope. The S0$ envelope here is that of a struck instrument. Note that the first value in S0$ is 15 for shortest Attack, then a 12 to provide a slower decay, three 08's for sustain, and then 04 and 00 for a slower release. You will certainly notice the difference in tones when you run the program; in fact, the switch from envelope to no envelope is itself a pleasing effect.
Program 2 offers a somewhat different effect by playing two chords with and without the envelope.
Program 3 introduces the effect of harmonics on a single note and again gives a side-by-side comparison. These are the even harmonics found in pianos. Note several points here. In most instruments the fundamental frequency is the loudest, then the harmonics. And the fourth harmonic may be louder than the second. In real instruments there are both odd and even harmonics. A string plucked in the center produces a different sound than a string plucked near the end. I have ignored both of these points in this program.
Program 4 is similar to Program 3 except that it provides odd harmonics with and without the ADSR envelope. Program 5 compares even and odd harmonics with the envelope. In both programs I have ignored the complications-or let's say that I have created a musical sound that cannot be duplicated by a musical instrument.
Remember, the objective of this article was to show ways to add color to your sounds, not to synthesize the Boston Symphony Orchestra. So let me give you some further suggestions. In any of these programs, change line 20 to FOR I=8 TO 1 STEP - 1 and you will have a sound that can be duplicated only by playing a tape recorder backwards. How about adding odd and even harmonics of the same fundamental frequency? Perhaps instead of having the Release part of the envelope go to 00, it would go back up to 15. How about using one of the sound channels to add the slight bit of noise that goes along with some instruments?
Please refer to "COMPUTE!'s Guide To Typing In Programs" before entering these listings.
Program 1: Notes With And Without ADSR
Envelope
PK 0 GOTO 100
KM 10 REM Sound envelope
AK 20 FOR I=1 TO 25
CN 21 TRAP 23:R=VAL(S0$(2*I-1,2*I)>;T
RAP 40000
LE 22 POKE 53761,160+R-POKE 53763,160
+R:POKE 53765,160+R:POKE 53767,
160+R:NEXT I
EF 23 RETURN
NI 100 DIM S0$ (50)
OB 110 S0$="1512080808040200"
JD 190 POKE 53760,243
HE 200 GOSUB 20
JE 290 POKE 53760,162
HF 300 GOSUB 20
AE 305 Q=1^1^1^1
IN 310 POKE 53760,243
OJ 312 POKE 53761,168:Q=1^1:POKE 5376
1,0
IP 330 POKE 53760,162
OL 332 POKE 53761, 168: Q=1^1:POKE 5376
1,0
AD 340 Q=1^1^1^1
GL 350 GOTO 190
LF 1000 REM Same tones with and witho
ut envelope
Program 2: Chords With And Without ADSR
Envelope
PK 0 GOTO 100
KM 10 REM Sound envelope
NL 20 FOR I=1 TO 8
CN 21 TRAP 23:R=VAL(S0$(2*I-1,2*I)):T
RAP 40000
LE 22 POKE 53761,160+R:POKE 53763,160
+R:POKE 53765,160+R:POKE 53767,
160+R:NEXT I
EF 23 RETURN
MI 100 DIM S0$(50)
0B 110 S0$="1512080808040200"
DH 190 POKE 53760,243-POKE 53762,193:
POKE 53764,144:POKE 53766,121
HE 200 GOSUB 20
DG 290 POKE 53760,243:POKE 53762,182:
POKE 53764,144:POKE 53766,121
HF 300 GOSUB 20
AE 305 Q=1^1^1^1
CM 310 POKE 53260,243:POKE 53762,193:
POKE 53764,144:POKE 53766,121
FD 312 POKE 53761,168:POKE 53763,168:
POKE 53765,168:PDKE 56767,168
OD 320 Q=1^1
DE 322 POKE 53761,160:POKE 53763,160:
POKE 53765,160:POKE 56767,160
CH 330 POKE 53260,243:POKE 53762,182:
POKE 53764,144:POKE 53766,121
FF 332 POKE 53761,168:POKE 53763,168:
POKE 53765,168:POKE 56767,168
AD 340 Q=1^1^1^1
GL 350 GOTO 190
MD 1000 REM Two chords with and witho
ut envelope
Program 3: Even Harmonics With And
Without ADSR Envelope
PK 0 GOTO 100
KM 10 REM Sound envelope
NL 20 FOR I=1 TO 8
CN 21 TRAP 23:R=VAL(S0$(2*I-1,2*I)):T
RAP 40000
LE 22 POKE 53761,160+R:POKE 53763,160
+R:POKE 53765,160+R:POKE 53767,
160+R:NEXT I
EF 23 RETURN
MI 100 DIM S0$(50)
OB 110 S0$="1512080808040200"
ML 190 POKE 53760,243-POKE 53762,121:
POKE 53764,60:POKE 53766,40
HE 200 GOSUB 20
KE 290 POKE 53760,162:POKE 53762,81:P
OKE 53764,40:POKE 53766,27
HF 300 GOSUB 20
AE 305 Q=1^1^1^1
MF 310 POKE 53760,243:POKE 53762,121:
POKE 53764,60:POKE 53766,40
FD 312 POKE 53761,168:POKE 53763,168:
POKE 53765,168:POKE 56767,168
OD 320 Q=1^1
DE 322 POKE 53761,160:POKE 53763,160:
POKE 53765,160:POKE 56767,160
JP 330 POKE 53760,162:POKE 53762,81:P
OKE 53764,40:POKE 53766,27
FF 332 POKE 53761,168:POKE 53763,168:
POKE 53765,168:POKE 56767,168
AD 340 Q=1^1^1^1
GL 350 GOTO 190
MD 1000 REM Even harmonics envelope a
nd no envelope
Program 4: Odd Harmonics With And
Without ADSR Envelope
PK 0 GOTO 100
KM 10 REM Sound envelope
NL 20 FOR I=1 TO 8
CN 21 TRAP 23:R=VAL(S0$(2*I-1,2*I)):T
RAP 40000
LE 22 POKE 53761,160+R:POKE 53763,160
+R:POKE 53765,160+R:POKE 53767,
160+R:NEXT I
EF 23 RETURN
NI 100 DIM S0$(50)
OB 110 S0$="1512080808040200"
KL 190 POKE 53760,243-POKE 53762,81:P
OKE 53764,49:POKE 53766,35
HE 200 GOSUB 20
KB 290 POKE 53760,162:POKE 53762,54:P
OKE 53764,32:POKE 53766,23
NF 300 GOSUB 20
AE 305 Q=1^1^1^1
KF 310 POKE 53760,243-POKE 53762,81:P
OKE 53764,49:POKE 53766,35
FD 312 POKE 53761,168:POKE 53763,168:
POKE 53765,168:POKE 56767,168
OD 320 Q=1^1
DE 322 POKE 53761,160:POKE 53763,160:
POKE 53765,160:POKE 56767,160
JN 330 POKE 53760,162-POKE 53762,54:P
OKE 53764,32:POKE 53766,23
FF 332 POKE 53761,168:POKE 53763,168:
POKE 53765,168:POKE 56767,168
AD 340 Q=1^1^1^1
GL 350 GOTO 190
EN 1000 REM Odd harmonics envelope an
d no envelope
Program 5: Even And Odd Harmonics With
ADSR Envelope
PK 0 GOTO 100
KM 10 REM Sound envelope
NL 20 FOR I=1 TO 8
CN 21 TRAP 23:R=VAL(S0$(2*I-1,2*I)):T
RAP 40000
LE 22 POKE 53761,160+R:POKE 53763,160
+R:POKE 53765,160+R:POKE 53767,
160+R:NEXT I
EF 23 RETURN
MI 100 DIM S0$(50)
OB 110 S0$="1512080808040200"
KL 190 POKE 53760,243:POKE 53762,81:P
OKE 53764,49:POKE 53766,35
HE 200 GOSUB 20
KB 290 POKE 53760,162:POKE 53762,54:P
OKE 53764,32:POKE 53766,23
HF 300 GOSUB 20
AE 305 Q=1^1^1^1
MF 310 POKE 53760,243:POKE 53762,121:
POKE 53764,60:POKE 53766,40
HI 312 GOSUB 20
JP 330 POKE 53760,162:POKE 53762,81:P
OKE 53764,40:POKE 53766,27
HK 332 GOSUB 20
AD 340 Q=1^1^1^1
GL 350 GOTO 190
HL 1000 REM Odd and even harmonics wi
th envelope