MACHINE LANGUAGE
Jim Butterfield, Associate Editor
Multiplication
Part 1
Many microprocessors don't have a multiplication instruction, including the 6502. But to do math, to efficiently handle tables, or even to input a multidigit number, a program must be fruitful, and multiply.
Classic Simplicity
The easiest way to perform multiplication is repeated addition. This is much too simple, and we tend to avoid it. Yet for very small numbers it can be reasonably efficient. If you have a small number in X and wish to multiply the contents of address $0390 by X, placing the results into addresses $0391 (high) and $0392 (low), you might code:
LDA #$00 STA $0391 LOOP CPX #$00 BEQ EXIT DEX CLC ADC $0390 BCC LOOP INC $0391 BCS LOOP ; complete the job here EXIT STA $0392
It's very simple. If the result is known to fit into a single byte, the coding can be shortened even more. If X contains a high value, however, this kind of program becomes time-consuming.
To examine the classic method of multiplication, we should try an example in decimal notation to see how it works:
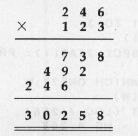
The steps are: multiplying (by each digit), shifting over to a new column, and addition. Exactly the same steps will be used in binary, but they become simpler. Multiplication will be either times 0 or times 1 (giving zero or the original multiplicand). Shifting a column changes to shifting a bit; this could be a left or right rotation depending on which way we're going. And addition can be performed by the ADC command as we generate the various intermediate products. Let's look at some simple binary multiplication.
Multiplying Bits
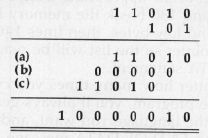
The decimal equivalent of this multiplication is 26 X 5 equals 130; but it's more interesting to see the binary workings. The intermediate values that we add (lines a and c) correspond to the original multiplicand, appropriately shifted. There's a zero in there too (line b), but a multiplication program wouldn't go to the trouble of adding zero. Instead, it would skip the addition.
It doesn't matter in principle if we shift the multiplicand left or right; we'll end up with the same result. In practice, we usually employ a trick. We don't shift the multiplicand at all; instead, we shift the product as it is generated. Thus, we would work the above example backwards: We would start with line (c) and put the value 11010 into the product area. Backing up to line (b), we'd shift the product left (giving 110100). The appropriate multiplier bit would be zero, so we'd skip the addition. Back up to line (a), shifting the product again (and getting 1101000). Now we spot a 1 bit at the right of the multiplier, so we add the multiplicand once again; 1101000 plus 11010 gives 10000010, our answer.
We'll talk more about the general multiplication procedure next time. By extracting the same logic for specific numbers, we can generate very fast multiplication algorithms.
For example, often you'll need to multiply a number by ten decimal. If a program receives decimal values typed in by the user, each digit will be added to the previous value times ten. Example: If the user has typed in 23 and now types 4, the 23 must be multiplied by ten to give 230; then we add the 4 to get 234.
A Shifty Solution
Let's examine the binary representation for ten decimal: 1010. If we keep in mind the procedure described above, we can do the job easily. Start with the high bit (1, of course). Starting with a product of zero, add in the value to be multiplied by ten. (For the sake of example, let's say that it is 23.) Shift it left; since the next bit is a zero, we won't add. Shift it left again (by this time the 23 has achieved a value of 92); the next bit of the multiplier is a 1, so we add the original value of 23 (giving 115). Shift left again; the final bit is zero, so no addition. Result: 230.
You might like to try your hand at working through the logic of multiplying by 60—binary 111100. It ends up as add (or load); shift-add; shift-add; shift-add; shift; shift.
Shifts become "long shifts" when applied to numbers over one byte long. ASL becomes ASL-ROL for two bytes, or ASL-ROL-ROL for three bytes. Depending on the programmer's knowledge of the values, it may be necessary to check for overflow—the result may be too big to fit the space provided.
Let's write a simple routine for a Commodore machine to input a two-digit decimal number. We'll need to multiply the first digit by ten.
; print question mark LDA #$3F JSR $FFD2 ; get first digit DIG1 JSR $FFE4 ; reject illegal keys CMP #$30 BCC DIG1 CMP #$3A BCS DIG1 ; echo and convert to binary JSR $FFD2 AND #$0F ; store in work area; multiply by ten STA $0380 ASL A ASL A ADC $0330 ASL A
Note that we don't need to check for overflow or clear the carry flag before addition. We know the digit is less than ten; we know that the shifts will produce values well within one byte's range, and that the carry will be cleared by the shifts.
; store results; get next digit STA $0380 D1G2 JSR $FFE4 ; reject illegal keys CMP #$30 BCC DIG2 CMP #$3A BCS D1G2 ; echo and convert to binary JSR $FFD2 AND #$0F ; add previous digit CLC ADC $0380
The two-digit number is now a binary value in the A register. The program will probably continue by storing it somewhere. There's no ambiguity on size: The result fits within one byte, since it can't be over 99.
Next month we'll talk about general multiplication: any number by any other number.