Programming 64 Sound
Part 1
John Michael Lane
This in-depth look at sound for the 64 provides you with practical methods for controlling the 64's SID chip from BASIC. This two-part article starts off with a brief discussion of sound and music in general.
Sight and sound are two essential components of successful computer games. Though the methods used to produce visual images differ from one computer to another, it is not too hard to produce an image that looks something like what you want. When designing space games, it's really easy, because just about anything can look like a spaceship.
Producing sound, however, can be quite a different matter. How can you produce the sound of a laser gun when dealing with such unfamiliar concepts as frequency, waveforms, and envelopes? (Actually lasers don't make any noise, but you know the sound I mean.)
Without a pretty expensive test setup, it can seem impossible to produce exactly the sound you're looking for. The only recourse is trial and error. Still, if you understand a little about the physics of sound and how it relates to the sound generator you're using, you can produce creditable results.
Real Sound
Sound is produced when physical objects vibrate. Vibrations are then set in motion in the air and travel through the air as sound waves to our ears. Sound, in its purest form, has only two physical attributes, frequency and amplitude. Frequency, the number of vibrations per second, is usually measured in cycles per second, or hertz. The higher the frequency or pitch of the sound, the higher a note sounds to our ears.
We've probably never heard a tone that consisted purely of one frequency. Physical objects also create vibrations at frequencies which are multiples of a fundamental frequency. The presence and quantity of these overtones determine the tonal quality, the color or timbre, of the sound. It's this tonal quality that determines whether a noise we hear sounds like a banjo or a drum (although there are other factors which we'll get to in a minute).
Different instruments and objects produce these overtones in varying amounts. Some produce strong overtones which are even multiples of the fundamental frequency. Some produce tones which are rich in the odd multiples. There really is no limit to the variety of tonal qualities that exist in the real world.
On some organs, and on some music synthesizers, you can specify the exact amount of each overtone you want included in each sound. On the synthesizer included in the Commodore 64, this is handled through the different types of waveforms that can be selected. But how does a waveform relate to tonal quality?
Waveforms
Figure 1 shows a sine wave at the fundamental frequency (all pure tones are sine waves) and at the first overtone or second harmonic. Notice that when we add the two waveforms together, the result no longer exactly resembles a sine wave. In Figure 2 we have continued adding sine waves of higher harmonics. You can see now that the resulting total waveshape is beginning to resemble a sawtooth, one of the waveforms available from the Commodore 64's Sound Interface Device (SID). If we kept adding the higher harmonics until we reached infinity, we would have a perfect sawtooth.
Figure 1: Fundamental And Sound Harmonics Combined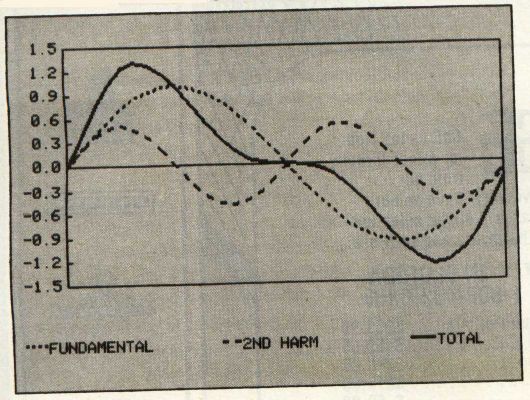
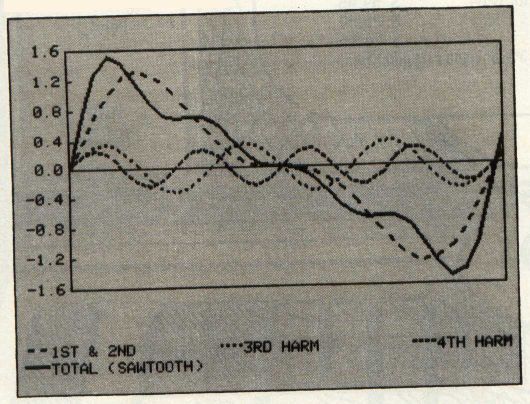
So the shape of the wave actually defines the harmonic content of the sound. Since all pure tones are sine waves, the shape of the wave generated by a sound synthesizer is actually assembled from sine waves that are multiples of the fundamental frequency.
The Commodore 64's SID has a choice of three basic waveforms and white noise, which is a collection of random frequencies. The three waveforms are a triangular wave, a rectangular pulse wave, and a sawtooth wave. The rectangular pulse wave also has a variable pulse width or duty cycle, which allows you additional freedom to vary the color of the sound produced. None of these waveshapes corresponds exactly to the sound produced by any instrument. It is also impossible to duplicate the complex harmonics of a real instrument simply by choosing one of these three waveforms. They do, nevertheless, give you the flexibility to produce a wide variety of color content, and you can get close to the particular sound you're seeking.
The harmonic content of the triangular wave diminishes very quickly, and the color of the wave consists almost entirely of the fundamental frequency. The sawtooth wave is the richest in terms of harmonics and the square wave falls in between. However, since the pulse width of the pulse wave can be varied, it can also contain a great variety of harmonic content.
Sound Envelopes
Earlier we said that sound consists of two qualities, frequency and amplitude. We've discussed primary frequency and how harmonic overtones are defined by the shape of the wave, but what about amplitude or loudness?
We don't mean how loud the sound is simply in the sense of volume, but rather how quickly the sound rises to its full strength and how quickly it dies down again to silence.
If you play an organ, you know that the sound of a note almost immediately reaches its full strength after you press the key and just as quickly dies down when you release the key. To our ears, it's just about instantaneous.
This is quite different from plucking a guitar string, where the sound quickly (but not quite instantaneously) reaches its full height and then slowly dies down, so that the tone continues several seconds after the note was struck. Violins, xylophones, banjos, and woodwinds all are different in the way that the sound rises, is sustained, and then dies down. Generally, these qualities are referred to as the envelope of the sound.
Figure 3: Waveform Shapes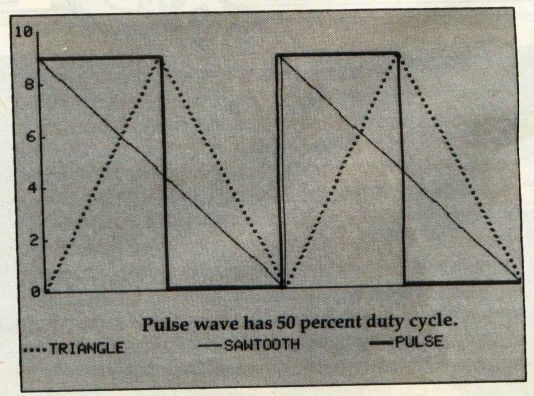
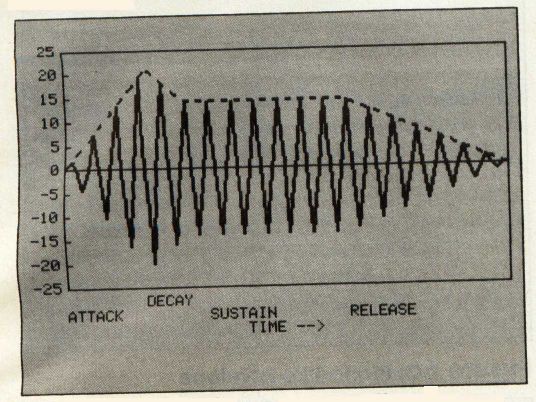
If you look at Figure 4, you will see how a sound looks it you could teed it into an oscilloscope. We can see the shape of the wave. The shape of the envelope defines the characteristics of a sound in a manner very similar to the way that harmonic content defines a sound.
The Commodore 64 uses a four-part sound envelope (see Figure 5). The first phase, called the attack, is the length of time it takes for the sound to reach its full volume. The second phase is the decay. During this phase, the sound decreases from the peak achieved during the attack phase to the level set for the sustain phase. During the third or sustain phase, the volume remains constant. In the final phase, the release, the volume decreases to zero.
Figure 5: Attack/Decay/Sustain/Release Envelope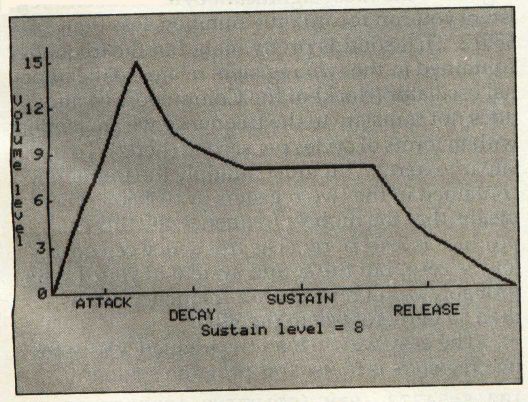
Not all sounds have this four-part volume envelope. Some have only an attack and release phase, and some (like the organ) have only the sustain phase. We can achieve all these on the Commodore 64 simply by setting the other phases to zero.
| Table 1: ADSR Envelope Values | |||
| VALUE | ATTACK RATE | DECAY RATE | RELEASE RATE |
| 0 | 2 ms | 6 ms | 6 ms |
| 1 | 8 ms | 24 ms | 24 ms |
| 2 | 16 ms | 48 ms | 48 ms |
| 3 | 24 ms | 72 ms | 72 ms |
| 4 | 38 ms | 114 ms | 114 ms |
| 5 | 56 ms | 168 ms | 168 ms |
| 6 | 68 ms | 204 ms | 204 ms |
| 7 | 80 ms | 240 ms | 240 ms |
| 8 | 100 ms | .3 sec | .3 sec |
| 9 | .25 sec | .75 sec | .75 sec |
| 10 | .5 sec | 1.5 sec | 1.5 sec |
| 11 | .8 sec | 2.4 sec | 2.4 sec |
| 12 | 1 sec | 3 sec | 3 sec |
| 13 | 3 sec | 9 sec | 9 sec |
| 14 | 5 sec | 15 sec | 15 sec |
| 15 | 8 sec | 24 sec | 24 sec |
The Commodore's SID allows us to set the attack, decay, and release phases to any one of 15 values or to zero. The times that correspond to the 15 values can be seen in Table 1. The times vary from milliseconds to seconds. Please note that the table does not include times for the sustain phase. The SID allows you to set a sustain volume level, but you must control the length of the sustain by opening and closing a gate. That gate is bit 0 of the fourth register in the SID chip. We'll cover this in greater detail later.
To turn the sound on in the SID chip, you must open the gate. As soon as the gate is opened, the sound level begins to rise at a rate determined by the attack. Once the peak level is reached, the sound begins to decline to the level set for the sustain. The rate at which it declines is defined by the decay.
However, if the sustain level is set at 15 (the highest choice), the decay phase is essentially meaningless because the sustain level and the peak of the attack phase are the same. Thus the decay phase has nowhere to decay to.
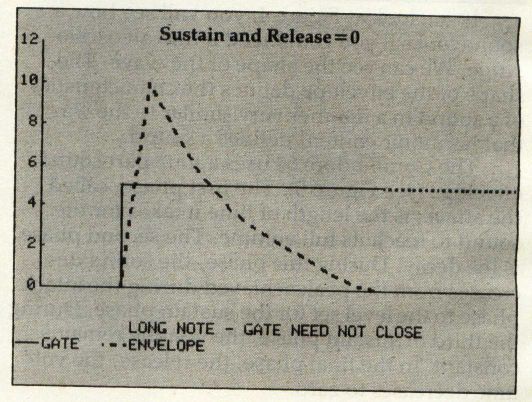
Once the decay phase is complete, the sustain cycle will continue as long as the gate is open. Once the gate is closed, the release phase begins and the volume falls from the level set for the sustain phase to zero. So, how long is the sustain phase?
Obviously, the sustain phase lasts as long as the time that the gate is open minus the time required for the attack and decay phases. If you close the gate too soon, you may have no sustain phase at all. If you close it really early, you'll cut short your decay or attack and decay phases as well. Figure 6 shows several combinations of attack, decay, and release values and how they interact with the gate to produce the sound envelope.
Figure 6: Standard Four-Part Envelope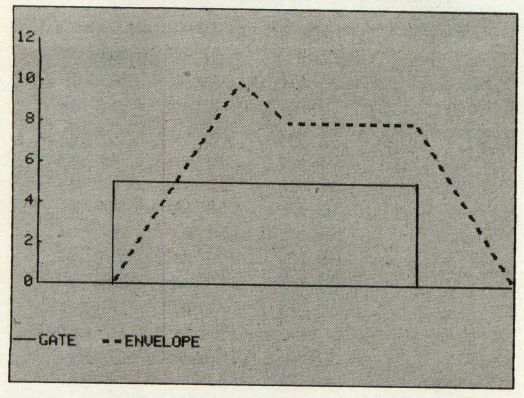
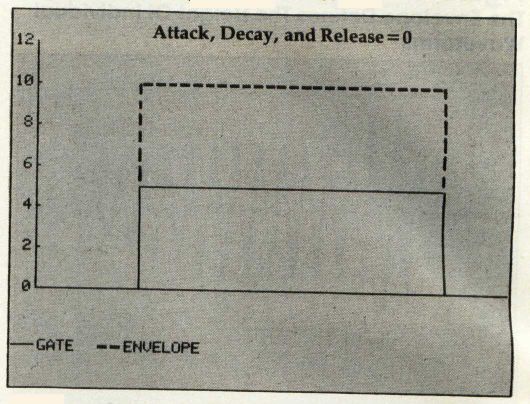
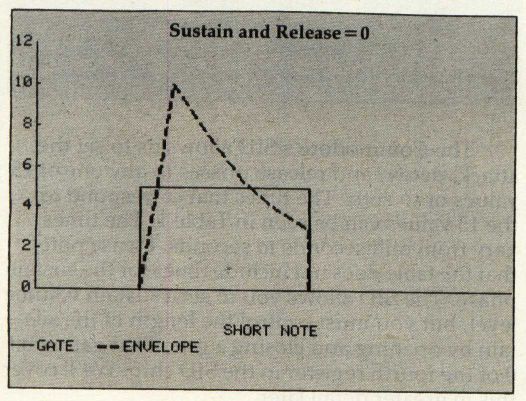
Programming Sound
The SID is really a quite amazing chip. It takes just 29 registers in your computer's memory, and with those 29 registers (actually you won't even use them all) you can produce a great variety of sounds. We'll call them registers, but they're actually a row of 29 bytes of memory.
For our purposes, we'll consider only the first 21 registers in the SID chip. We'll also briefly consider the twenty-fifth register, which sets the volume (no volume, no sound).
The first 21 registers break down into three groups of seven. That's because the SID has three voices, and the seven register groups perform almost the same function for all three voices. That makes it far easier—all we have to learn is how to program seven registers.
Table 2 gives the functions of the seven register groups. Registers 0 and 1 hold the frequency. Register 0 contains the least significant byte, and register 1 the most significant byte. With two registers you can record only numbers less than 65512. That sounds pretty high, but the frequency contained in the two registers relates to the internal oscillator (clock) of the Commodore 64 and does not translate to the frequency we are familiar with in terms of cycles per second (hertz). To translate into hertz, you must multiply the frequency contained in the two registers by .059605. This means that the highest frequency the SID can produce is 3904 hertz. The frequency can go as low as zero, but the sound system in your TV set probably won't reproduce a frequency of less than 50 hertz (or 840 to the SID).
The easy way to load the frequency into the two registers is to use this program segment:
100 S = 54272 : REM (STARTING ADDRESS OF SID
CHIP)
110 F0 = FR/.059605 : REM FR = FREQUENCY IN CYC
LES/SECOND
120 F2 = INT (F0/256) : F1 = F0-256 * F2
130 POKE S, F1 : POKE S + 1, F2
If you already know the frequency in terms of the SID chip, you can omit line 110.
Table 2: Map Of Sound Interface Device (SID) Registers
The next two registers contain the pulse width of the rectangular pulse wave. This value is a 12-bit number with the eight least significant bits stored in register 2, and the four most significant stored in bits 3—0 of register 3. The four remaining bits of register 3 are not used. If you are using something other than a rectangular pulse wave, you don't have to worry about these two registers.
The pulse width can take a value from 0 to 4095, which corresponds to a range of 0 to 100 percent for the duty cycle. A value of 2048 implies a 50 percent duty cycle and generates a square wave. If these two registers are set to zero and the rectangular pulse wave is selected, no sound will be produced.
The following program segment can be used to set the pulse width.
140 P0=DC*4095/100: REM DC=DUTY CYCLE IN % 150 P2=INT (P0/256): P1=P0-256*P2 160 POKE S+2, P1: POKE S+3, P2
We should add here that a duty cycle of 10 percent will sound exactly the same as a duty cycle of 90 percent. For some advanced applications the two may sound different, but for a solitary rectangular pulse wave voice, there will be no difference.
Next month we'll get into more complicated music programming.