TECHNIQUES FOR WRITING YOUR OWN ADVENTURE GAME
Charles Perkins
Adventure games are as intriguing to write as they are to play. Here are a few techniques to help you create an intricate drama without running out of memory. These suggestions are useful for any computer, but the specific examples concern Commodore computers.
Remember, you have other tools at your disposal beside standard PEEKs, POKEs, and IF...THENs when programming games. One-byte pointers and ragged tables, for example, can sometimes come in handy as techniques to save memory and help with complicated game logic.
Using these techniques, I developed an adventure game entirely in BASIC for my 8K Commodore PET 2001 (actually 7167 bytes of free memory). It includes an adventure with 48 rooms, 576 vocabulary words, 12 objects (trolls, witches, etc.), and many descriptors and interactive responses. The game is table driven, and the entire adventure, including vocabulary, is stored as data. Many different adventures can be developed using this same program without change.
Computer game programs often use numbers which do not exceed the range of 0 to 255. Array indices and loop variables are common examples. The typical personal computer running BASIC does not permit one-byte variables (value range 0-255). A variable (either floating point or integer) on my PET is always seven bytes long. If your game program needs a good amount of memory and you store lots of variables with values in the range of 0-255, then this unneeded overhead is a problem.
BASIC (which causes the problem) also offers a solution. String manipulation functions permit the program to address a single character, and a character is stored in a single byte (plus some overhead which will be discussed later). With these string manipulation functions and simple algorithms to convert characters to numbers and vice versa, it is possible to efficiently store numbers in one byte.
This approach is particularly useful when a game program makes extensive use of pointers. Pointers are stored variables which "point" to specific pieces of data (i.e., the indices of a table entry). The approach is easily extended to the creation and use of "ragged" tables. A ragged table is one in which the number of columns varies with each row.
One-Byte Pointers
In its simplest form, a one-byte pointer is a value between 0 and 255 stored as a corresponding character in a string variable. Given the character (C$), its value (C) is determined by the equation C = ASC(C$). Given the value, the appropriate character is determined by the function C$ = CHR$(C). Storing individual characters as individual strings is not efficient (it uses up eight bytes in the PET), so multiple variables must be stored together in a string (the overhead is constant, and each character adds only one additional byte of memory). To retrieve the Nth character from the storage string (A$), the equation is C$ = MID$(A$,N,1). To store a new value in the string is a bit more trouble, but it's still just string manipulation.
Storing The Variables
The simple code number approach described above works if the one-byte variables are always kept internally in the computer. If you want to store the variables on tape or examine them on the screen, a problem arises: the internal character codes include special characters which cannot be saved or printed. In fact, only 128 characters (seven bits) can be saved or printed, and one of these (the quote mark) has special meaning to the PET and cannot be used. The usable character set in the PET has code numbers between 32 and 95 and between 160 and 223. The quote mark is character 34.
In my adventure game application, the storage strings are input from tape as data. I also chose to reserve seven characters as special flags and to eliminate the quote mark from the allowed character set for positive numbers. As a result, I was forced to use slightly more complex encoding and decoding subroutines:
Given a character C$, then the value C is computed by:
10 C = ASC(C$) : C = C-40 + (C > 159)*64 : RETURN where (C > 159)= -1 if C > 159 and 0 if C= <159
Given a number D, then the character D$ is determined by:
20 IF D < 56 THEN D$ = CHR$(D + 40) : RETURN 30 D$ = CHR$(D + 104) : RETURN
These routines yield a range from -8 to 119 with the quote mark at -6. The negative values were used internally as the special flags in my adventure game. In these routines, an open parenthesis is a zero; a close parenthesis is 1. A shifted back arrow is 119; a blank is -8. The encoding and decoding subroutines may have to be revised for other computers, depending on the code number schemes used.
Passages And Exits
To understand how one-byte pointers can be used to save memory in your game programs, consider the simple adventure map in Figure 1. You start at a crossroad (state 1). Movement to the north, south, and west places you in a forest or in houses of various colors. There is a secret, one-way passage from the red house to the blue house. Going east from the crossroad puts you in a cave from which there is no escape.
This adventure map can be expressed as a state table, as shown in Table 1. The rows of the table correspond to states (locations) in the map. The columns correspond to the possible movement directions (in this case north, south, east, and west). If you are in state 1 (the crossroad) and wish to move south, you end up in state 5 (the red house). (This state transition is shown in Table 1.) A further attempt to move south (while in state 5) has no path ("no exit"), indicated by the zero pointer. All exits from state 4 (the cave) put you back in state 4. This would appear as an endless cave to the person playing the game.
The state table can be programmed into the adventure game using the subroutines described above. The result is shown in Table 2. This encoded state table requires only 42 bytes of memory in the PET (including all overhead, as discussed below). Storing the table as a matrix of integer numbers would require 59 bytes on the PET. While the memory saved is not dramatic for this small example, when large tables are used, the memory saved can be quite substantial.
Ragged Tables
Suppose that we wish to add descriptions of each state to our game program. These would be printed on the screen each time a state was entered. A list for our simple adventure game map is shown in Table 3.
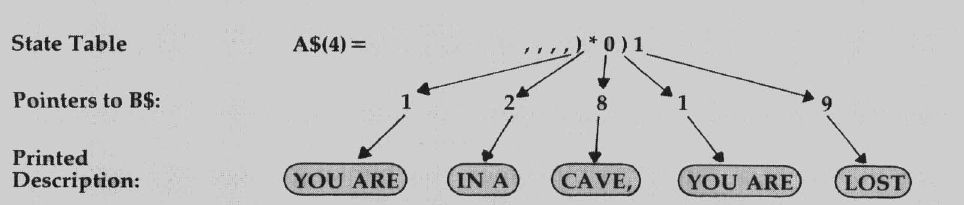
These could be stored in strings, but they would consume 118 bytes of memory (plus some overhead). Alternatively, these descriptions can be broken into phrases which are used in various combinations to make up the descriptions. These phrases are shown in Table 4. These phrases require only 53 bytes (plus some overhead), but we must also define the rules for combining phrases back into descriptions for each state. Once again, we use one-byte pointers. These new pointers can be simply added to the encoded state table, as shown in Table 5.
The procedure for creating a description when a state is entered is shown graphically in Figure 2. The BASIC code necessary to print the description of state 1 is as follows:
40 L = LEN(A$(I)) find length of string 50 FOR J = 5 TO L skip first four characters and scan 60 C$ = MID$(A$(I),J,1) select next character 70 GOSUB 10 convert to number C (see above) 80 PRINT B$(C)" "; print phrase and blank 90 NEXT J 100 PRINT end print line
Note that the number of characters in each state table entry shown in Table 5 is different. It is therefore a "ragged" table. It requires 18 additional bytes to store the pointers for all five state descriptions, a net savings of 47 bytes compared to storing the full descriptions (not including overhead).
Storage Methods
The techniques described above can be applied to computing problems other than games. The bigger the pointer tables are, the more advantages one-byte pointers offer. However, the tradeoff between one-byte pointers and simple integers is tricky because of the overhead required to set up strings or arrays of strings, and because extra programming is required to isolate and decode the stored character.
The storage technique used in my PET 2001 (original ROMs) requires seven bytes plus the number of characters for string variables. Thus, a single character pointer should never be used. When arrays are used, the tradeoff is dependent upon the number of rows and columns involved. For a ten by ten two-dimensional array, the memory used for a floating point array is 509 bytes. This is 500 bytes for the numbers and nine bytes for an array header (overhead). An integer array requires 209 bytes (200 bytes for the numbers and nine bytes for the header).
Using the one-byte variables reduces this array to a one-dimensional array of ten strings. Each string is ten characters long. The total memory requirement is 137 bytes. This is 100 bytes for the numbers, seven bytes for the header, three bytes for each string, for a total of 37 bytes overhead. As the arrays get larger, the one-byte approach uses approximately one-half the memory required by integer arrays and one-fifth of the memory required by floating point arrays. A more detailed explanation of the storage structures of Commodore computers can be found in Programming The PET (COMPUTE! Books, 1982).
The one-byte storage technique can be especially useful when: memory is at a premium, when large tables of pointers are needed, and when ragged tables provide a programming advantage.
When you're programming games into computers with limited memory (such as the unexpanded VIC-20), these techniques can be very advantageous.
Figure 1: Adventure Map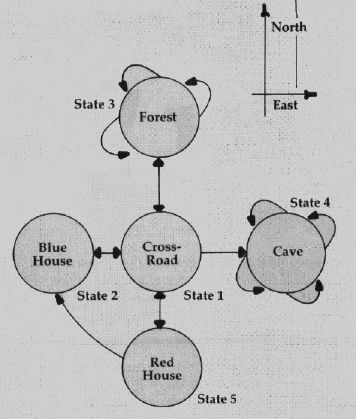
| Table 1: State Table For The Adventure Map | |||||
| Movement Direction | |||||
| State | North | South | East | West | |
| 1 | 3 | 5 | 4 | 2 59 bytes | |
| 2 | 0 | 0 | 1 | 0 required | |
| 3 | 3 | 1 | 3 | 3 in PET | |
| State | 4 | 4 | 4 | 4 | 4 to store |
| Transition | 5 | 1 | 0 | 0 | 2 as integers |
| Table 2: Encoded State Table | |
| A$(l) = + - , * | |
| A$(2) = (() ( | 42 bytes |
| A$(3) = + ) + + | required |
| A$(4) = , , , , | in PET |
| A$(5) = )((* |
| Table 3: State Descriptions | |
| State 1 "YOU ARE AT A CROSSROAD" | |
| State 2 "YOU ARE IN A BLUE HOUSE" | 118 bytes |
| State 3 "YOU ARE IN A FOREST" | required plus |
| State 4 "YOU ARE IN A CAVE, YOU ARE LOST" | overhead |
| State 5 "YOU ARE IN A RED HOUSE" |
| Table 4: Phrase Table | |
| B$(l) = "YOU ARE" | |
| B$(2) = "IN A" | |
| B$(3) = "AT A CROSSROAD" | |
| B$(4) = "BLUE" | 53 bytes |
| B$(5) = "RED" | required |
| B$(6) = "HOUSE" | plus |
| B$(7) = "FOREST" | overhead |
| B$(8) = "CAVE," | |
| B$(9) = "LOST" |
| Table 5: Ragged State Table With Descriptor Pointers | |
| A$(l)= + - ,*) + | |
| A$(2)= ( () ()*,. | |
| A$(3)= + ) + + )*/ | 18 added bytes |
| A$(4)= ,,,,)* 0)1 | for a total of |
| A$(5)= )((*)*-. | 60 bytes |
 |
required |
| pointers | in PET |
| to phrase | |
| table |