Education
Friends Of The Turtle
David D. Thornburg
Innovision
Los Altos, CA
Welcome to a new Society – the Friends of the Turtle. A free membership in this society is available to all subscribers to this magazine, and our meetings will be held on these pages every issue. The goal of this society is to promote the type of computer graphics and robot environment that uses what is called "turtle geometry."
Turtle geometry is a key element in several user-friendly computer languages such as Atari PILOT, TI LOGO, and Apple LOGO. It may come as a surprise to some of you, but the types of graphics commands used in these languages are also obeyed by a programmable toy – the Milton Bradley Big Trak. Turtle geometry encourages exploration. It can be learned by first-time computer users of almost any age, and its power is so great that it can keep full-fledged computer wizards engrossed for years. The turtle is a graphics tool that makes it easy for you to get the computer to do what you want it to do.
In these pages we will share programs that illustrate many interesting ideas and developments in this field. Most of all, we will share beautiful designs that have come out of this computer environment.
Background – What Is A Turtle?
If you have ever played with a Milton Bradley Big Trak, or used computer languages like Atari PILOT, LOGO, or WSFN, you have encountered a very special device called a turtle. Basically, a turtle is a "robot" that can move around the floor (or display screen) in response to messages you send it. Display turtles often have "pens" with which they can leave traces of their path as they move. This makes the turtle a handy tool for drawing pictures.
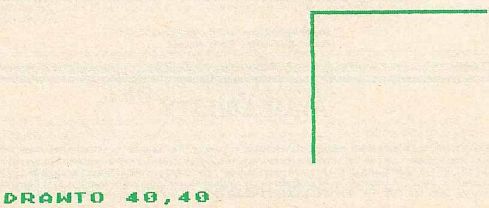
The difference between turtle graphics and conventional coordinate graphics can be demonstrated by drawing a square in both systems.

In coordinate geometry, the pen is moved to various coordinates on a grid. To draw a square 40 units on a side, we could use these five steps:
GOTO 0, 0 (put the pen at the origin) DRAWTO 0, 40 (draw the left vertical line) DRAWTO 40,40 (draw the top horizontal line) DRAWTO 40,0 (draw the right vertical line) DRAWTO 0,0 (draw the bottom horizontal line)
This is illustrated below.
Figure 1a.



Next, let's see how a square would be drawn in turtle geometry. We make the turtle draw lines by giving a sequence of instructions like this:
REPEAT 4 (repeat the following commands 4 times) FORWARD 40 (draw a line 40 units long) RIGHT 90 (turn 90 degrees to the right)Figure 2.
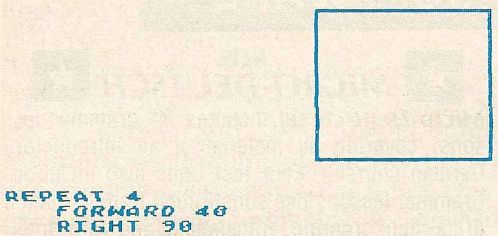
While the turtle commands that draw a square are much simpler than the commands in coordinate geometry, this is far from being their only power. The coordinate representation we showed only describes a square with vertical and horizontal sides. Suppose you wanted to draw a square tilted at some angle (say 30 degrees). How would you draw that in coordinate geometry?
In turtle geometry, the description of one square is just the same as that for any other square, independent of its orientation. To draw a square tilted at 30 degrees, you first must turn the turtle by 30 degrees before having it draw the square.
Figure 3.
The commands look like this:
RIGHT 30 REPEAT 4 FORWARD 40 RIGHT 90
The power of turtle geometry is so great that we cannot begin to touch it in this first column. If you want more information between now and the next "meeting," you should read "Picture This! PILOT'S Turtle Graphics for Atari" in the May-June 1981, issue of Recreational Computing. Two important books on this topic have recently been published – Mindstorms: Children, Computers, and Powerful Ideas by Seymour Papert (Basic Books), and Turtle Geometry: The Computer as a Medium for Exploring Mathematics by Harold Abelson and Andrea diSessa (MIT Press). A new book (by the author), Picture This!, will be published by Addison Wesley in early 1982. This book focuses on the Turtle Language incorporated into Atari PILOT.
Why Do We Need Friends Of The Turtle?
As we said before, turtle geometry is being incorporated in many of the computer languages that are just now beginning to be available on low-cost personal computers. Each of the various implementations of this environment has its special features and limitations. To the extent that the graphics environments in all these implementation are similar to each other, Friends of the Turtle will be a place where we can explore the turtle world ii. a machine independent fashion. We will describe all sorts of interesting experiments to do with turtles (since experimenting is probably the best way to learn geometry anyway), share our programs, provide a "Rosetta Stone" for various dialects of turtle languages, keep track of recent developments in the field, and generally have a good time. This last point is the most important, since the turtle is a marvelous device to play with.
So, welcome to friends of the Turtle. Please write to me with your ideas and programs. If you are new to this field you should know that we will spend a great deal of time dealing with the basics.
Turtles are for everyone, and so is this society Please write to me at the following address:
David D. Thornburg
Friends of the Turtle
P.O.Box 1317
Los Altos, CA 94022
