A Floating-Point Binary To BCD Routine
Marvin L. DeJong
Department of Mathematics-Physics
The School of the Ozarks
Pt. Lookout, MO 65726
Introduction
A previous issue of COMPUTE! carried a BCD to Floating-Point Binary Routine that can be used to convert a series of decimal digits and a decimal exponent to a binary number in a floating-point format. The purpose of such a routine is to enable the user to perform floatingpoint arithmetic. The program described in this article performs the reverse operation; that is, it converts a floating-point binary number to a decimal number and a decimal exponent. With these two routines and an Am9511 Arithmetic Processing Unit one can do most of the functions found on scientific calculators. I hope to provide a few simple arithmetic routines in the near future. In the meanwhile, you can amuse yourself by converting numbers to floatingpoint binary numbers and then back to decimal numbers.
Hindsight
The BCD to floating-point binary routine described previously used a divide-by-ten routine that was part of the main program. With my excellent hindsight I now realize that the divide-by-ten routine should have been written as a subroutine, to be called by both the BCD to floating-point binary routine and the binary to decimal routine described here. So my first task was to rewrite the divide-by-ten routine as a subroutine. I also discovered that the divide-by-ten routine described in the previous article did not give sufficient precision. In any case, the divide-by-ten routine was completely revised and appears in Listing 1 in this article. It uses the location $0000, called OVFLO, as a "guard" byte to give the necessary precision. It actually starts at $0EC5, but our listing starts at $0EBF to indiciate a few changes that must be made in the original listing to insert the subroutine.
| Listing 1. A New Divide-by-Ten Routine. | ||||
| $OEBF 20 C5 0E | ONCMOR | JSR DIVTEN | Jump to divide-by-ten subroutine. | |
| 0EC2 B8 | CLV | Force a jump around the routine. | ||
| 0EC3 50 51 | BVC ARND | The new subroutine is inserted here. Clear accumulator for use as a register. Do $28 = 40 bit divide. OVFLO will be used as "guard" byte. | ||
| 0EC5 A9 00 | DIVTEN | LDA $00 | ||
| 0EC7 A0 28 | LDY $28 | |||
| 0EC9 06 00 | BRA | ASL OVFLO | ||
| 0ECB 26 04 | ROL LSB | |||
| 0ECD 26 03 | ROL NLSB | Roll one bit at a time into the accumulator which serves to hold the partial dividend. | ||
| 0ECF 26 02 | ROL NMSB | |||
| 0ED1 26 01 | ROL MSB | |||
| 0ED3 2A | ROL A | Check to see if A is larger than the divisor, $0A = 10. | ||
| 0ED4 C9 0A | CMP $0A | |||
| 0ED6 90 05 | BCC BRB | No. Decrease the bit counter. | ||
| 0ED8 38 | SEC | Yes. Subtract divisor from A. | ||
| 0ED9 E9 0A | SBC $0A | |||
| 0EDB E6 00 | INC OVFLO | Set a bit in the quotient. | ||
| 0EDD 88 | BRB | DEY | Decrease the bit counter. | |
| 0EDE D0 E9 | BNE BRA | |||
| 0EE0 C6 05 | BRC | DEC BEXP | Division is finished, now normalize. | |
| 0EE2 06 00 | ASL OVFLO | For each shift left, decrease the binary exponent. | ||
| 0EE4 26 04 | ROL LSB | |||
| 0EE6 26 03 | ROL NLSB | Rotate the mantissa left until a one is in the most-significant bit. | ||
| 0EE8 26 02 | ROL NMSB | |||
| 0EEA 26 01 | ROL MSB | |||
| 0EEC 10 F2 | BPL BRC | |||
| 0EEE A5 00 | LDA OVFLO | If the most-significant bit in the guard byte is one, round up. | ||
| 0EF0 10 12 | BPL BRE | |||
| 0EF2 38 | SEC | Add one. | ||
| 0EF3 A2 04 | LDX $04 | X is byte counter. | ||
| 0EF5 B5 00 | BRD | LDA ACC, X | Get the LSB. | |
| 0EF7 69 00 | ADC $00 | Add the carry. | ||
| 0EF9 95 00 | STA ACC, X | Result into mantissa. | ||
| 0EFB CA | DEX | |||
| 0EFC DO F7 | BNE BRD | Back to complete addition. | ||
| 0EFE 90 04 | BCC BRE | No carry from MSB so finish. | ||
| 0F00 66 01 | ROR MSB | A carry, put in bit seven, and increase the binary exponent. | ||
| 0F02 E6 05 | INC BEXP | |||
| 0F04 A9 00 | BRE | LDA $00 | Clear the OVFLO position, then get out. | |
| 0F06 85 00 | STA OVFLO | |||
| 0F08 60 | RTS | |||
| . | . | |||
| . | . | Empty memory locations here. | ||
| . | . | |||
| 0F16 A9 00 | ARND | LDA $00 | Remainder of BCD-to-floating | |
| . | . | |||
| : | : | point routine is here. |
| Listing 2. Modifications to the BCD-to-Floating-Point Binary Routine. | |||
| $0E54 18 | CLC | Clear carry for addition. | |
| 0E55 A5 05 | LDA BEXP | Get binary exponent. | |
| 0E57 69 20 | ADC $20 | Add $20 = 32 to place binary | |
| 0E59 85 05 | STA BEXP | point properly. | |
| 0E5A EA | NOP | ||
| 0E5B EA | NOP | ||
| $0D53 A0 20 | BR7 | LDY $20 | Y will limit the number of left shifts to 32. |
| 0D55 A5 01 | BR10 | LDA MSB | |
| 0D57 30 0D | BMI BR11 | If mantissa has a one in its most-significant bit, get out. | |
| 0D59 18 | CLC | ||
| 0D5A A2 04 | LDX $04 | ||
| 0D5C 36 00 | BR9 | ROL ACC,X | Shift accumulator left one bit. |
| 0D5E CA | DEX | ||
| 0D5F D0 FB | BNE BR9 | ||
| 0D61 C6 05 | DEC BEXP | Decrement binary exponent for each left shift. | |
| OD63 88 | DEY | ||
| 0D64 D0 EF | BNE BR10 | No more than $20 = 32 bits shifted. | |
| 0D66 60 | BR11 | RTS | That's it. |
Some other minor modifications to the program are given in Listing 2. Although the BCD to Floating-Point Binary program will work without these changes, it will work better if you introduce the changes shown in Listing 2. The development of the program described in this article enabled me to find some places to improve the other routine. The modifications are simple and short.
The Conversion Routine
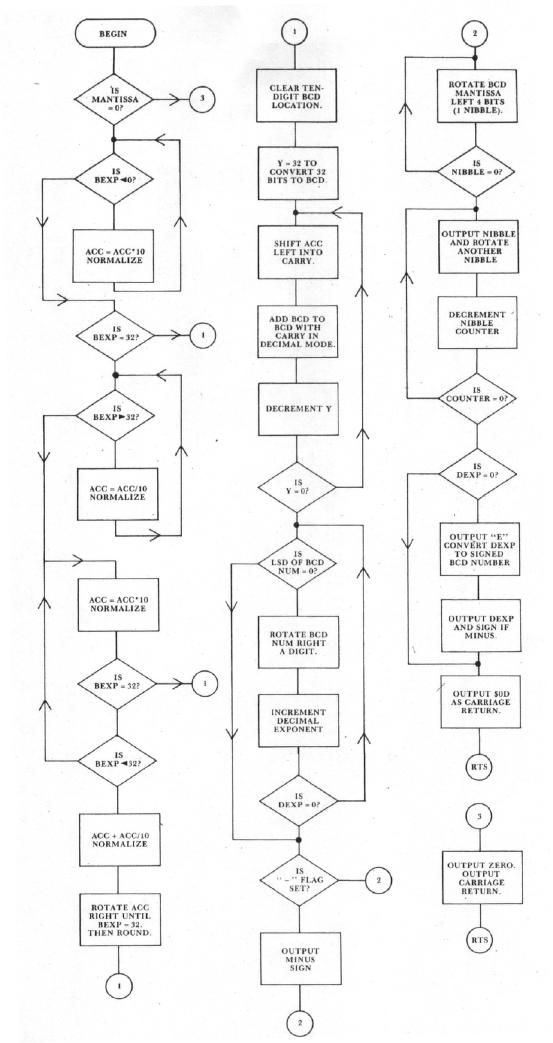
The program to convert a normalized floating-point binary number and its exponent to a BCD number and then output the result is given in Listing 3. A 32-bit binary to BCD conversion subroutine is called by this program and it is found in Listing 5. A flowchart of the entire process is given in Figure 1. The normalized floating-point binary mantissa is operated on by a series of "times ten" or "divide by ten" operations until the binary point is moved from the left of the mantissa to the right of the 32 bit mantissa. In other words, we multiply by ten or divide by ten until the binary exponent is 32. Then the mantissa represents an integer and can be converted to a BCD number using the subroutine in Listing 5. The algorithm for this latter routine is from Peatman's (John B)
| Listing 3. A Floating-Point Binary to BCD Routine. | |||
| $0B00 A5 01 | BEGIN | LDA MSB | Test MSB to see if mantissa is zero. |
| 0B02 D0 0E | BNE BRT | If it is, print a zero and then get out. Clear display. | |
| 0B04 20 9B 0F | JSR CLDISP | ||
| 0B07 A9 30 | LDA $30 | Get ASCII zero. | |
| 0B09 20 A6 0F | JSR OUTCH | Jump to output subroutine. | |
| 0B0C A9 0D | LDA $0D | Get "carriage return." | |
| 0B0E 20 A6 0F | JSR OUTCH | Output it. | |
| 0B11 60 | RTS | Return to calling routine. | |
| 0B12 A9 00 | BRT | LDA $00 | Clear OVFLO location. |
| 0B14 85 00 | STA OVFLO | ||
| 0B16 A5 05 | BRY | LDA BEXP | Is the binary exponent negative? |
| 0B18 10 0B | BPL BRZ | No. | |
| 0B1A 20 00 0D | JSR TENX | Yes. Multiply by ten until the exponent is not negative. | |
| 0B1D 20 30 0D | JSR NORM | ||
| 0B20 C6 17 | DEC DEXP | Decrement decimal exponent. | |
| 0B22 B8 | CLV | Force a jump. | |
| 0B23 50 Fl | BVC BRY | Repeat. | |
| 0B25 A5 05 | BRZ | LDA BEXP | Compare the binary exponent to |
| 0B27 C9 20 | CMP $20 | $20 = 32. | |
| 0B29 F0 48 | BEQ BCD | Equal. Convert binary to BCD. | |
| 0B2B 90 08 | BCC BRX | Less than. | |
| 0B2D 20 C5 0E | JSR DIVTEN | Greater than. Divide by ten until BEXP is less than 32. | |
| 0B30 E6 17 | INC DEXP | ||
| 0B32 B8 | CLV | Force a jump. | |
| 0B33 50 F0 | BVC BRZ | ||
| 0B35 A9 00 | LDA $00 | Clear OVFLO | |
| 0B37 85 00 | STA OVFLO | ||
| 0B39 20 00 0D | BRW | JSR TENX | Multiply by ten. |
| 0B3C 20 30 0D | JSR NORM | Then normalize. | |
| 0B3F C6 17 | DEC DEXP | Decrement decimal exponent. | |
| 0B41 A5 05 | LDA BEXP | Test binary exponent. | |
| 0B43 C9 20 | CMP $20 | Is it 32? | |
| 0B45 F0 2C | BEQ BCD | Yes. | |
| 0B47 90 F0 | BCC BRW | It's less than 32 so multiply by 10. | |
| 0B49 20 C5 0E | JSR DIVTEN | It's greater than 32 so divide. | |
| 0B4C E6 17 | INC DEXP | Increment decimal exponent. | |
| 0B4E A5 05 | BRU | LDA BEXP | Test binary exponent. |
| 0B50 C9 20 | CMP $20 | Compare with 32. | |
| 0B52 F0 0F | BEQ BRV | Shift mantissa right until exponent | |
| 0B54 46 01 | LSR MSB | is 32. | |
| 0B56 66 02 | ROR NMSB | ||
| 0B58 66 03 | ROR NLSB | ||
| 0B5A 66 04 | ROR LSB | ||
| 0B5C 66 0B | ROR TEMP | Least-significant bit into TEMP. | |
| 0B5E E6 05 | INC BEXP | Increment exponent for each shift | |
| 0B60 B8 | CLV | right. | |
| 0B61 50 EB | BVC BRU | ||
| 0B63 A5 0B | BRV | LDA TEMP | Test to see if we need to round |
| 0B65 10 0C | BPL BCD | up. No. | |
| 0B67 38 | SEC | Yes. Add one to mantissa. | |
| 0B68 A2 04 | LDX $04 | ||
| 0B6A B5 00 | BRS | LDA ACC,X | |
| 0B6C 69 00 | ADC $00 | ||
| 0B6E 95 00 | STA ACC,X | ||
| 0B70 CA | DEX | ||
| 0B71 D0 F7 | BNE BRS | ||
| 0B 73 20 67 0D | BCD | JSR CONVD | Jump to 32 bit binary-to-BCD routine. |
| 0B76 A0 04 | BRM | LDY $04 | Rotate BCD accumulator right until non-significant zeros are shifted out or DEXP is zero, whichever comes first. |
| 0B78 A2 04 | BRP | LDX $04 | |
| 0B7A 18 | CLC | ||
| 0B7B 76 20 | BRQ | ROR BCDN.X | |
| 0B7D CA | DEX | ||
| 0B7E 10 FB | BPL BRQ | ||
| 0B80 88 | DEY | ||
| 0B81 D0 F5 | BNE BRP | ||
| 0B83 E6 17 | INC DEXP | Increment exponent for each shift right. Get out when DEXP = 0. | |
| 0B85 F0 06 | BEQ BRO | ||
| 0B87 A5 20 | LDA LBCDN | Has a non-zero digit been shifted into the least-significant place? | |
| 0B89 29 0F | AND $0F | ||
| 0B8B F0 E9 | BEQ BRM | No. Shift another digit. | |
| 0B8D EA | BRO | NOP | Oops. These NOPs cover an earlier mistake. |
| 0B8E EA | NOP | ||
| 0B8F EA | NOP | ||
| 0B90 EA | NOP | ||
| 0B91 EA | NOP | ||
| 0B92 20 9B 0F | JSR CLDISP | This routine simply clears the AIM 65 20-character display. | |
| 0B95 A5 07 | LDA MFLAG | ||
| 0B97 F0 05 | BEQ BRN | If the sign of the number is minus, output a minus sign first. | |
| 0B99 A9 2D | LDA $2D | ||
| 0B9B 20 A6 0F | JSR OUTCH | ASCII " - " = $2D. Output character. | |
| 0B9E A9 0B | BRN | LDA $0B | Set digit counter to eleven. |
| 0BA0 85 0B | STA TEMP | ||
| 0BA2 A0 04 | BRI | LDY $04 | Rotate BCD accumulator left to output most-significant digits first. But first bypass zeros. |
| 0BA4 18 | BRH | CLC | |
| 0BA5 A2 FB | LDX $FB | ||
| 0BA7 36 25 | BRG | ROL BCDN | |
| 0BA9 E8 | INX | ||
| 0BAA D0 FB | BNE BRG | ||
| 0BAC 26 00 | ROL OVFLO | Rotate digit into OVFLO. | |
| 0BAE 88 | DEY | ||
| 0BAF D0 F3 | BNE BRH | ||
| 0BB1 C6 0B | DEC TEMP | Decrement digit counter. | |
| 0BB3 A5 00 | LDA OVFLO | Is the rotated digit zero? | |
| 0BB5 F0 Eb | BEQ BRI | Yes. Rotate again. | |
| 0BB7 18 | BRX | CLC | Convert digit to ASCII and output it. |
| 0BB8 69 30 | ADC $30 | ||
| 0BBA 20 A6 0F | JSR OUTCH | ||
| 0BBD A9 00 | LDA $00 | Clear OVFLO for next digit. | |
| 0BBF 85 00 | STA OVFLO | ||
| 0BC1 A0 04 | LDY $04 | Output the remaining digits. | |
| 0BC3 18 | BRL | CLC | |
| 0BC4 A2 | $FB | LDX $FB | |
| 0BC6 36 25 | BRJ | ROL BCDN,X | Rotate a digit at a time into |
| 0BC8 E8 | INX | OVFLO, then output it. One digit is four bits or one nibble. | |
| 0BC9 D0 FB | BNE BRJ | ||
| 0BCB 26 00 | ROL OVFLO | ||
| 0BCD 88 | DEY | ||
| 0BCE D0 F3 | BNE BRL | ||
| 0BD0 A5 00 | LDA OVFLO | Get digit. | |
| 0BD2 C6 0B | DEC TEMP | Decrement digit counter. | |
| 0BD4 D0 E1 | BNE BRX | ||
| 0BD6 A5 17 | LDA DEXP | Is the decimal exponent zero? | |
| 0BD8 F0 48 | BEQ ARND | Yes. No need to output exponent. | |
| 0BDA A9 2E | LDA $2E | Get ASCII decimal point. | |
| 0BDC 20 A6 2E | JSR OUTCH | Output it. | |
| 0BDF A9 45 | LDA $45 | Get ASCII "E". | |
| 0BE1 20 A6 0F | JSR OUTCH | ||
| 0BE4 A5 17 | LDA DEXP | Is the decimal exponent plus? | |
| 0BE6 10 0D | BPL THERE | Yes. | |
| 0BE8 A9 2D | LDA $2D | No. Output ASCII " - " | |
| 0BEA 20 A6 0F | JSR OUTCH | ||
| 0BED A5 17 | LDA DEXP | It's minus, so complement it and add one to form the twos complement. | |
| 0BEF 49 FF | EOR $FF | ||
| 0BF1 85 17 | STA DEXP | ||
| 0BF3 E6 17 | INC DEXP | ||
| 0BF5 A9 00 | THERE | LDA $00 | Clear OVFLO. |
| 0BF7 85 00 | STA OVFLO | ||
| 0BF9 F8 | SED | Convert exponent to BCD. | |
| 0BFA A0 08 | LDY $08 | ||
| 0BFC 26 17 | BR1 | ROL DEXP | |
| 0BFE A5 00 | LDA OVFLO | ||
| $0C00 65 00 | ADC OVFLO | ||
| 0C02 85 00 | STA OVFLO | ||
| 0C04 88 | DEY | ||
| 0C05 D0 F5 | BNE BR1 | ||
| 0C07 D8 | CLD | ||
| 0C08 18 | CLC | ||
| 0C09 A5 00 | LDA OVFLO | Get BCD exponent. | |
| 0C0B 29 F0 | AND $F0 | $Mask low-order nibble (digit). | |
| 0COD F0 09 | BEQ BR2 | ||
| 0C0F 6A | ROR A | Rotate nibble to the right. | |
| 0C10 6A | ROR A | ||
| 0C11 6A | ROR A | ||
| 0C12 6A | ROR A | ||
| 0C13 69 30 | ADC $30 | Convert to ASCII. | |
| 0C15 20 A6 OF | JSR OUTCH | Output the most-significant digit. | |
| 0C18 A5 00 | BR2 | LDA OVFLO | Get the least-significant digit. |
| 0C1A 29 0F | AND $0F | Mast the high nibble. | |
| 0C1C 18 | CLC | ||
| 0C1D 69 30 | ADC $30 | Convert to ASCII. | |
| 0C1F 20 A6 0F | JSR OUTCH | ||
| 0C22 A9 0D | ARND | LDA $0D | Get an ASCII carriage return. |
| 0C24 20 A6 0F | JSR OUTCH | ||
| 0C27 60 | RTS | All finished. |
Microprocessor Based Design
(McGraw-Hill).
Of course, each time the binary number is multiplied by ten or divided by ten the decimal exponent is adjusted. Thus, we are left with a BCD number in locations $0020 - $0024 (five locations for ten digits) and a decimal exponent in $0017. The rest of the routine is largely processing required to give a reasonable output format. Since we don't want to print a group of non-significant zeros, the BCD number is rotated right until all the zeros are shifted out or the decimal exponent is zero, whichever comes first.
Next the routine starts examining the BCD number from the left and skips any leading zeros. Thus, the first non-zero digit is the first digit printed. Of course, if the number is minus (a non-zero result in location $0007) a minus sign is printed. Next the decimal point is printed, and finally the exponent is printed in the form "E XX." Thus, the format chosen always has the decimal point to the right of the significant digits, 3148159. E-6 for example. If you want scientific notation for non-integer results you can modify the output routine. It's simply a matter of moving the decimal point. The flowchart and the comments should allow you to understand and modify the code.
| Listing 4. Subroutine OUTCH For the AIM 65. | |||
| $OFA6 20 00 F0 | OUTCH | JSR PRINT | AIM 65 monitor subroutine. |
| OFA9 20 72 0F | JSR MODIFY | See previous article in COMPUTE! | |
| 0FAC 20 60 0F | JSR DISPLAY | See previous article in COMPUTE! | |
| 0FAF 60 RTS | RTS |
| Listing 5. A 32 Bit Binary-to-BCD Subroutine. | |||
| $0D67 A2 05 | CONVD | LDX $05 | Clear BCD accumulator. |
| 0D69 A9 00 | LDA $00 | ||
| 0D6B 95 20 | BRM | STA BCDA,X | Zeros into BCD accumulator. |
| 0D6D CA | DEX | ||
| 0D6E 10 FB | BPL BRM | ||
| 0D70 F8 | SED | Decimal mode for add. | |
| 0D71 A0 20 | LDY $20 | Y has number of bits to be converted. Rotate binary number into carry. | |
| 0D73 06 04 | BRN | ASL LSB | |
| 0D75 26 03 | ROL NLSB | ||
| 0D77 26 02 | ROL NMSB | ||
| 0D79 26 01 | ROL MSB | ||
| D7B A2 FB | LDX $FB | X will control a five byte addition. Get least-significant byte of the BCD accumulator, add is to itself, then store. | |
| 0D7D B5 25 | BRO | LDA BCDA,X | |
| 0D7F 75 25 | ADC BCDA,X | ||
| 0D81 95 25 | STA BCDA,X | ||
| 0D83 E8 | INX | Repeat until all five bytes have been added. | |
| 0D84 D0 F7 | BNE BRO | ||
| 0D86 88 | DEY | Get another bit from the binary number. | |
| 0D87 D0 EA | BNE BRN | ||
| 0D89 D8 | CLD | Back to binary mode. | |
| 0D8A 60 | RTS | And back to the program. |