BOOT CAMP
It's hard to believe, but here we are in the seventh installment of Boot Camp. We've only got a few more 6502 operation codes to cover before we begin writing full-scale programs, so hang in! The best is yet to come.
Old
Business
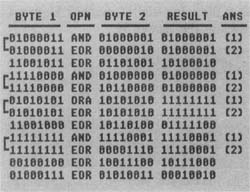
Last issue's assignment asked you to solve eight
bit-manipulation problems. You were given "before" and "after" bit
patterns and asked to find what operation codes and operands were used
to get the results. Figure 1
shows the completed assignment. Some of the problems had two possible
answers. These are so noted, with both solutions.Clever readers have probably noticed that the fourth problem actually has far more than two possible answers. In fact, by using the ORA instruction, Byte 2 could be any value with bits 1, 3, 5 and 7 set! Try it yourself with a short program.
Simple
Multiplication
As you may recall, by shifting a binary number left one bit, we effectively multiply it by two. Shifting it left two bits multiplies it by four. This principle is very handy, allowing us to multiply integers quickly and easily.
How do we perform this left-shift operation in 6502 assembly language? With the ASL (Arithmetic Shift Left) instruction, of course. This operation shifts the contents of the accumulator or a selected memory byte left one bit, and has the following formats:
ASL A (ACCUMULATOR)
ASL nn (ABSOLUTE)
ASL n (ZERO PAGE)
ASL n,X (ZERO PAGE INDEXED X)
ASL nn,X (INDEXED X)
When an ASL instruction is executed, the accumulator or memory byte is shifted one bit to the left. Figure 2 shows how the operation is handled internally.

As you can see from the "before" and "after" images in Figure 2, each bit of the selected byte is shifted to the left one place. Since Bit 8 has no other place to go, it is shifted into the 6502 Carry flag. This is done to allow for multiple-byte shifts, which we'll look at in a moment. A 0 is shifted into the 1 bit. As you can see, the value of the byte has been multiplied by two!
As long as the results of your shiftmultiples do not exceed 255 decimal, you will find the ASL instruction works fine. Problems begin, though, when you get into multiple-byte values.
Figure 3 shows an example of a multiplebyte shift. As you can see, the contents of Bit 7 of the low byte must shift into Bit 0 of the high byte. In order to do this, we must see the LSR instruction to shift the low byte, and a new instruction, ROL (Rotate Left through carry), for the high byte. ROL has the following formats:

ROL A ACCUMULATOR)
ROL nn (ABSOLUTE)
ROL n (ZERO PAGE)
ROL n,X (ZERO PAGE INDEXED X)
ROL nn,X (INDEXED X)
The ROL instruction performs the same function as ASL, except that it puts the contents of the Carry flag in the low-order bit instead of a zero.
Both ASL and ROL set the Sign, Zero and Carry flags according to the result of the operation.
Let's look at a few examples of multiplication using the ASL and ROL instructions.
| 10 *= $0600 20 LDA #$07 ;PLACE 7 IN ACCUM. 30 ASL A ;TIMES 2 40 ASL A ;TIMES 4 50 ASL A ;TIMES 8 60 STA TIMES8 ;SAVE RESULT 70 BRK ;AND STOP! 80 TIMES8 *=*+1 90 .END |
The above shows an example of singlebyte multiplication using the ASL instruction. In this example, we're multiplying the contents of the accumulator (7) by eight and storing the result in the location labeled TIMES8.
Line 20 loads the accumulator with the number 7 (00000111 binary). You can try different values here to test the multiply. Remember that since this is only a single-byte multiply, the result cannot exceed 255. Therefore, don't use any values greater than 31 decimal here.
Line 30 shifts the accumulator to the left one bit, multiplying the accumulator by two. After this instruction executes, the accumulator will contain 14 decimal (00011110 binary).
Line 40 shifts the accumulator left another bit. At this point, the accumulator is four times the starting value of 7, or 28 (00011100 binary).
Line 50 shifts the accumulator left a third time, giving us eight times the starting value, or 56 (00111000 binary).
Line 60 stores the final value of 56 decimal ($38 hex) in the location labeled TIMES8. If you change the value in line 20, the value you enter will be multiplied by eight and placed in TIMES8.
Line 70 stops the program execution.
Line 80 reserves one byte for the result of the multiplication, labeled TIMES8.
The above example shows how easy the ASL instruction makes it to multiply a number by a power of two, but what if you want to multiply a number by five?
In such cases, it's good to break the multiplier down into "bite-sized" pieces. For example, a multiply by five can be broken down into:
| (NUMBER * 4) + (NUMBER ) ----------- (NUMBER * 5) |
The 6502 code required for this operation is shown below.
| 10 *= $0600 15 LDA #23 ;PLACE 23 IN ACCUM. 20 ASL A ;TIMES 2 25 ASL A ;TIMES 4 30 CLC ;CLEAR CARRY FOR ADD 35 ADC #23 ;ADD 23 = TIMES 5! 40 STA TIMES5 ;AND STORE RESULT 45 BRK ;ALL DONE! 50 TIMES5 *=*+1 55 .END |
Similarly, a multiply by ten can be broken down to:
|
(NUMBER * 8) + (NUMBER * 2) ------------ (NUMBER * 10) |
With its 6502 code shown here:
| 10 *= $0600 15 LDA #23 ;PLACE 23 IN ACCUM. 20 ASL A ;TIMES 2 25 STA TIMES2 ;SAVE *2 VALUE 30 ASL A ;TIMES 4 35 ASL A ;TIMES 8 40 CLC ;CLEAR CARRY FOR ADD 45 ADC TIMES2 ;*8 + *2 = *10! 50 STA TIMES10 ;SAVE TIMES 10 55 BRK ;AND STOP! 60 TIMES2 *=*+1 65 TIMES10 *=*+1 70 .END |
As you can see, you can multiply a number by almost any value through a combination of left-shifts and add/subtract operations. It's just a matter of careful planning when writing a program.
Multi-Byte
Multiplication
Now that we've looked at single-byte multiplication,
we can go on to bigger and better things, such as multiplying two-byte
values. The figure below shows the procedure for multiplying the
two-byte value TOTAL by 16. Note that the low-order byte is always
SHIFTed, and the high byte is always ROTATEd.| 10 *= $0600 15 LDA #$02 ;PLACE 02 ... 20 STA TOTAL+1 ;IN TOTAL HI BYTE 25 LDA #$4F ;PLACE 4F... 30 STA TOTAL ;IN TOTAL LO BYTE 35 ASL TOTAL ;SHIFT LOW, 40 ROL TOTAL+1 ;ROTATE HI = TIMES 2 45 ASL TOTAL ;SHIFT LOW, 50 ROL TOTAL+1 ;ROTATE HI = TIMES 4 55 ASL TOTAL ;SHIFT LOW, 60 ROL TOTAL+1 ;ROTATE HI = TIMES 8 65 ASL TOTAL ;SHIFT LOW, 70 ROL TOTAL+1 ;ROTATE HI = TIMES 16 75 BRK ;ALL DONE! 80 TOTAL *=*+2 85 .END |
Lines 15-30 initialize the variable TOTAL to $02417 (0000001001001111) binary. Note that the label TOTAL is the loworder byte and TOTAL+1 is the highorder byte.
Line 35 shifts the low byte of TOTAL left one bit, multiplying it by two. This operation places the contents of Bit 7 of the low byte in the Carry flag so that it can be shifted into the high byte by the next operation.
Line 40 rotates the high byte of TOTAL left, placing the Carry flag's con tents in Bit 0. Like the shift operation, the rotate places the contents of the high byte's Bit 7 in the Carry flag. After this instruction executes, TOTAL contains $049E (0000010010011110 binary), or two times the original value.
Lines 45-50 multiply TOTAL by two a second time, resulting in a value of $903( (0000100100111100 binary), or four times the original value.
Lines 55-60 multiply TOTAL by two again, giving a value of $1278 (0001001001111000 binary), or eight times the original value.
Lines 65-70 multiply TOTAL by two a final time, giving a final result of $24170 (0010010011110000 binary), which should be $02417*16. Checking, we find that $02417 is 591 decimal. 591 times 16 is 9456 decimal, or $24170, and our answer in TOTAL is correct.
These examples show the basics of 6502 multiplication, but don't stop here. Study the above code and try creating your own programming puzzles. I've given you the ball, now run with it!
Divide
and Conquer
Now that we've covered simple multiplication, let's
look at basic division. You know how bit-shifting works, so picking up
the finer points of binary division should be easy.Remember how shifting the value 49 decimal (00110001 binary) left one bit gave us 98 (01100010 binary)? What happens if we shift the value RIGHT one bit? Figure 4 gives us the answer.

As you can see, we've just discovered the first limitation of binary division-we can't handle decimals! Using real numbers instead of integers, 49/2 = 24.5. Shifting the value 49 right one bit divided it by two, all right, but we lost the decimal portion of the result. We'll look at real-number division in later installments of Boot Camp, but for now the loss of the precision does not matter. I mentioned the problem because it's good for you to be aware of this limitation.
In the 6502 instruction set, the operation that performs this right-shift is the LSR (Logical shift right) instruction. Its formats are:
| LSR A
(ACCUMULATOR) LSR nn (ABSOLUTE) LSR n (ZERO PAGE) LSR n,X (ZERO PAGE INDEXED X) LSR nn,X (INDEXI l) X) |
As Figure 4 shows, the LSR instruction shifts all the bits of the indicated byte right one position. A zero is placed in the highorder, or 128, bit. The low-order, or 1, bit is shifted into the Carry flag. This allows us to perform multi-byte right-shifts, similar to multi-byte left-shifts.
Before we look at multiple-byte division, let's look at a single-byte example.
10 *= $0600
20 LDA #184 ;PUT 184 IN ACCUM.
30 LSR A ;DIVIDE BY 2
40 LSR A ;DIVIDE BY 4
50 LSR A ;DIVIDE BY 8
60 STA DIV8 ;SAVE RESULT
70 BRK ;AND STOP!
80 DIV8 *-*+1
90 .END
The above shows an example of dividing a single-byte value by eight. Like multiplication by eight, this operation requires three shifts, but in the opposite direction. In this example, we divide the number 184 decimal by eight, placing the result in the location DIV8.
Line 20 places the number 184 (10111000 binary) in the accumulator.
Line 30 shifts the accumulator contents right one bit, dividing the value there by two. After this instruction, the accumulator contains 92 (01011100 binary).
Line 40 shifts the accumulator right another bit, dividing the value by two again. At this point the accumulator is divided by four and contains 46 (00101110 binary).
Line 50 shifts the accumulator right a final time, leaving the accumulator con'; raining the original value divided by eight. At this point it contains 23 (00010111 binary).
Line 60 stores the contents of the accumulator in the locaiton labeled DIV8. If you examine this location after the program executes, you will see that it contains 23 decimal ($17 hex). Checking, you will find that this is 184 divided by eight.
Line 70 BREAKS the program, stopping execution.
Line 80 reserves one byte for the value DIV8.
Now you see how simple single-byte division is. If you want to divide any integer up to 255 by a power of two, this process works fine.
Shifting
Into High
Up till now, we've limited ourselves to simple,
single-byte division. Now let's see how we do it with more than one
byte.Figure 5 shows the division of the twobyte value 28008 by two. As you can easily calculate, the result is 14004. If you compare this example with the multi-byte multiplication shown in Figure 3, you will notice an interesting difference.

In multiplication, the low byte is shifted and the high byte(s) is (are) rotated. This is because the bit-shift proceeds from right to left.
In division, however, things are reversed. Since we are shifting all the bits to the right, the highest byte is shifted and the remaining bytes are rotated. This allows the loworder bits of the bytes being divided to shift into the lower-order bytes.
Let's look at an example of the three-byte value SCORE being divided by four. The code necessary is shown below:
| 10 *= $0606 15 LDA #$49 ;SET UP ... 20 STA SCORE+2 ;3-BYTE... 25 LDA #$23 ;VALUE... 30 STA SCORE+1 ;IN SCORE... 35 LDA #$F8 ;= $4923F8 40 STA SCORE 45 LSR SCORE+2 ;DIVIDE... 50 ROR SCORE+1 ;SCORE... 55 ROR SCORE ;BY 2 60 LSR SCORE+2 ;DIVIDE... 65 ROR SCORE+1 ;SCORE... 70 ROR SCORE ;BY 4 75 BRK ;AND STOP! 80 SCORE *=*+3 85 .END |
Lines 15-40 initialize the three-byte value SCORE to $4923F8. Remember that multi-byte values are always stored in low-byte/high-byte order. In this case SCORE is the lowest-order byte and SCORE+2 is the highest-order byte.
Line 45 shifts the highest-order byte of SCORE right one bit. The 1-bit of SCORE+2 is placed in the Carry flag, ready to be rotated into the next byte of SCORE.
Line 50 rotates the middle-order byte right one bit. The bit carried from the highest-order byte is shifted into SCORE+1's 128-bit, and the 1-bit of SCORE+l is placed in the Carry flag for the next rotate.
Line 55 rotates the low-order byte of SCORE right one bit. Once again, the Carry status is placed in the 128-bit, and the 1-bit is shifted into the Carry. This final Carry is not used, but is ignored. After this instruction executes, the value in SCORE is divided by two and contains $2491FC. As an exercise, you can calculate the binary and decimal values.
Lines 60-70 perform the same function as Lines 45-55, leaving SCORE with the original value divided by four, or $1248FE. Calculate the decimal and binary values for this result, and you will see that the original value has been divided by four.
Line 75 BREAKS the execution of the program. At this point, you can examine the three bytes of SCORE and see that they contain the proper result.
Line 80 reserves three bytes for the variable SCORE.
Well, now you have the basics of integerbinary multiplication and division under your belt. The principle is simple; you just have to work with it until you feel comfortable. In order to do that, create your own problems to solve.
Here
it Comes
For those of you who need some prompting to get
started with problems, here's one that shouldn't be too hard if you've
read carefully.Write a program that multiplies the value 5 by 27. Use any of the techniques we have discussed so far. There are several possible solutions to this problem, so give it your best shot.
Next issue, we'll look at a couple of possible solutions. We'll also find out what the stack is and how it helps us write subroutines.