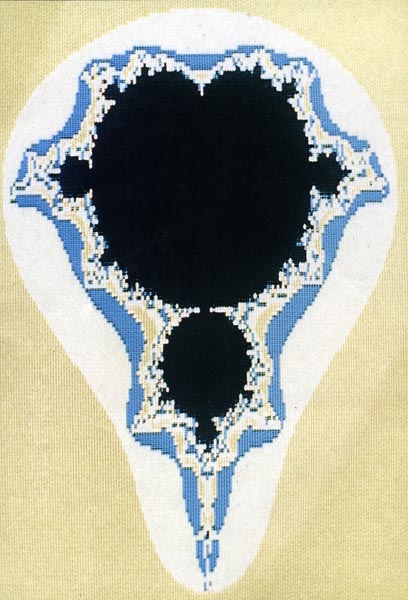
The Mandlebrot Set
FOR THE 8-BIT
USERby James J. Greco
In August of 1985 I received my issue of Scientific American. Inside it, in the "Computer Recreations" column by A.K. Dewdney, I found some fascinating computer-generated graphics, and the instructions for generating them. They were images of something called the Mandelbrot Set.
A brief look at the formula and method for generating these images told me that it was intended for a computer very unlike mine (an Atari 800 XL), a very expensive one.
In January of 1986 I received my issue of ANALOG Computing. To my surprise it contained a program for generating the Mandelbrot Set. There was hope my little Atari could produce these images after all! Hope was lost when I realized that the program was written for the 520ST. At that point I decided I was going to generate some of those images with a program I was going to have to write myself.
I went back to the Scientific American to find out exactly what the Mandelbrot Set was. If it were not for Mr. Dewdney's excellent article, I am sure I would not have ever found out. What follows is my attempt at explaining how they are generated.
The Mandelbrot Set is based on the repeated squaring of complex numbers. Complex numbers are numbers that involve the square root of - l. The square root of - 1 is represented by the letter i, for imaginary. If i is the square root of - 1, then i squared must be -1, a real number again. A complex number is a combination of the regular numbers we use every day (real numbers) and imaginary numbers. This combination is the addition of the two. Therefore 2 + 3i is a complex number, as is .00531 +2131. As a sideline, even the real numbers are considered complex, as they can be expressed as a real number plus 0i.
Addition of complex numbers is easy. All that needs to be done is to add the individual like parts (add the real parts together. then add the imaginary parts together), for example: (2 + 3i) + (4 + 7i) = 6 + 10i.
As I mentioned above, the Mandelbrot Set is generated by the repeated squaring of complex numbers. An example will probably best serve to demonstrate the squaring of complex numbers. To square 2 + 3i we expand it to (2 + 3i)*(2 + 3i). Multiplying this out we get: 4 + 6i + 6i + 9i2. collecting like terms we get 4 + 12i + 9i2. As I mentioned before i squared is -1. This means that 9i2 = - 9, a real number again. Substituting -9 into the above complex number and collecting all the real parts we get: - 5 + 12i.
Pairs of numbers can be plotted on a plane-this plane has two axes, a horizontal one and a vertical one. Complex numbers can also be plotted on a plane, called the complex plane. The complex plane has a real (horizontal) and an imaginary (vertical) axis.
The Mandelbrot Set is plotted on this complex plane. It seems that if certain complex numbers are continually squared, they will never exceed the size of two. The size of a complex number is the distance of that complex number from the origin. The origin is at (0,0i). The distance can be calculated by use of the Pythagorean theorem. If we take the sum of the squares of the sides, then take the square root of that, we will arrive at the size of that complex number. The numbers that never exceed the size of two are what make up the Mandelbrot Set. Most of the numbers in the complex plane quickly exceed the size of two, soon after the squaring process begins. These are the numbers that give the Mandelbrot Set its colors. The numbers that lie in the Mandelbrot Set are plotted black. The other numbers are plotted with a color representative of the number of times the squaring process is repeated before the size exceeds two.
After
selecting the desired
graphics mode, you will be
asked for the coordinates, size
and iteration for the
pictue you wish to create. The
coordinates and size can be
determined from a map of the
set or, as will be discussed
shortly, from the program itself.
graphics mode, you will be
asked for the coordinates, size
and iteration for the
pictue you wish to create. The
coordinates and size can be
determined from a map of the
set or, as will be discussed
shortly, from the program itself.
Finding and plotting these numbers is the task of this program. The monitor screen is going to represent the complex plane, with each pixel on the screen corresponding to an individual complex number. The value of the pixel is determined by two factors: 1) the center of the area that you wish to view (specified by a real and an imaginary number), and 2) the size of the area you desire to view. The latter can be likened to magnification. After these parameters are entered, the program calculates the complex values, of each pixel. This is done in such a manner that the center of the screen represents the center specified by the entry of the real and the imaginary values entered. The size determines the range of values to either side (and top to bottom) of the center. Each pixel value is then processed in a manner, soon described, that calculates whether that value lies in the Mandelbrot Set (plotted black) or if that value should be plotted with a color.
The function that determines where this value lies is: Z2←Z+u where Z and u are both complex numbers that can be represented as follows: Z=ar+ai, u = br + bi, where r indicates real and i indicates imaginary. The values br and bi are the value of the pixel, the values ar and ai are initially set to zero. The arrow in Z2←Z + u indicates that the values Z and u are added, then squared. If the result of this squaring is less than two, the resultant real value is then put into ar. The resultant imaginary value is then put into ai and the constant values (for the pixel) of br and bi are then added to the new values of ar and ai, then squared again. This process continues until the size of Z2 exceeds two or until we can safely assume that the value will never exceed two. This repeated performing of the same function is referred to as iteration. At the beginning of the program, you will be asked for the iteration limit. This is what determines the number of times the function will be implemented before it is assumed that a point lies in the Mandelbrot Set (assuming that the size does not first exceed two).
If the size does exceed two, the number of times it took to do so is used to determine the color that the pixel will be plotted with. The entire process is repeated for every pixel on the screen. If the area you want to look at lies entirely in the Mandelbrot Set (a very boring picture), and you choose 100 as the iteration limit in high-resolution mode, it would take 160*170*100 (2,720,000) calculations to complete the picture. This is why it takes more than a little time for this program to run.
About
the program
When you first run the program, you will be asked if
you want to save a screen, view a screen, complete a saved screen, see
directory (disk version) or none of the above. If you're going to want
to save the picture you're going to create, then select the save
option. Selecting the view option allows you to view a screen that you
have already saved. If, after you have started to create a screen that
you are planning to save, you decide you want to turn off the computer,
you can save a partial picture by pressing the HELP key. When this key
is pressed, the computer dumps the current values and the portion of
the screen that is completed to the I/O device (as soon as the line it
is working on is completed). To complete the screen at a later time,
choose the complete saved screen option from the menu. Simply pressing
RETURN will allow you to create a picture, but it can not be saved. If
you select the save option, you'll be prompted to insert your disk or
cassette at this time. If you're using a cassette recorder, it will
have to remain on until the screen is complete. Disk-drive users may
remove their disk and turn off the drive; just turn on the drive and
insert the disk when the screen is complete. After selecting the
desired graphics mode, you will be asked for the coordinates, size and,
iteration limit for the picture you wish to create. The coordinates and
size can be determined from a map of the set or, as will be discussed
shortly, from the program itself. A good iteration limit seems to me to
be about 100; the higher the number you choose the longer the set will
take to calculate, however, it will be more detailed and accurate.After the set has been calculated, or retrieved from disk or cassette, a double cursor will appear. This cursor can be moved around by use of the arrow keys. Finer movement can be obtained by holding down the control key and the desired arrow key. After the cursor has been moved to a position of interest, holding down the RETURN key will return the screen to graphics 0, and will display the coordinates and sizes of the cursor's two squares. Following the prompts another set can be calculated in the same manner as the first. For an overall look at the Mandelbrot Set, enter the follwing: real -.75, imaginary 0 and a size of 3; the whole set will be plotted. This can be your map; just move the cursor to the area you desire to look at closer and press RETURN.
Entering
the program:
For disk users simply type in the program as listed.
Cassette users make the following changes.Change Line 60 to read:
60 IF LOR=1 THEN FF=8:DQ$="C
:":GOTO 560
Change Line 150 to read:
150 PRINT " TO COMPLETE SAVE
D SCREEN PRESS C"
Change Line 220 to read:
220 DC$="C"
Change the last statement of Line 10( to read:
DQ$="C:"
Delete the following lines: 200, 240, 250, 1275, 1290, 1300, 1340, 1350, 1360, 1370, 1380, 1390, 1400.
Add the following lines:
230 IF FF=4 THEN PRINT:PRINT
"CUE CASSETTE, PRESS PLAY,
THEN RETURN";:INPUT B$:GOTO
280
280 NAME$="C:":IF FF=8 THEN
PRINT "CUE TAPE, PRESS RECOR
D AND PLAY, THEN RETURN";:IN
PUT B$
285 IF LOR=1 THEN ? "WHEN CA
SSETTE STOPS LOADING SCREEN,
REPOSITION TAPE, PRESS RE
CORD AND PLAY"
287 IF LOR=1 THEN ? "PRESS R
ETURN WHEN READY";:INPUT B$
A word of warning to cassette users-this program can be very frustrating. It takes a long time to save and load the screens, and you will often have errors trying to load a screen that will make hours of computing time worthless.
Some
Final Words
The Mandelbrot Set has some properties that seem to
me (a person with a limited math background) to be very unusual. It is
infinitely complex; that is, no matter how high a magnification (small
a size) one chooses, the Set remains just as complex as it is at lower
magnification levels. This means that it has an infinite perimeter, yet
it encloses a finite area. The set is also self similar; that is, at
specific locations and levels of magnification, you will see shapes
that are similar to, but not exactly like, shapes seen at other
magnifications and locations.LISTING 1: BASIC
note: blue characters represent inverse video
UK 1 REM ****************************
WY 2 REM * 8-BIT MANDELBROT *
XC 3 REM * BY *
OY 4 REM * JAMES J. GRECO *
GM 5 REM * *
OV 6 REM * COPYRIGHT 1988 *
XG 7 REM * BY *
GV 8 REM * ANALOG COMPUTING *
05 9 REM ****************************
LQ 10 GOTO 100
VV 20 C=C+1:X=I*I-J*J+V:U=2*I*J+Z:IF C<IL
AND X*X+U*U<4 THEN J=U:I=X:GOTO 20
HE 30 T(G)=P(C):C=0:I=0:J=8:IF G<>Y THEN
G=G+1:V=Q<G):GOTO 20
FN 40 FOR G=0 TO Y:COLOR T(G):PLOT G,K:NE
XT G:G=0:K=K+1:V=Q(G):Z=R(K):IF PEEK(7
32)=17 THEN POKE 732,O:GOTO 560
UO 50 IF K<>F THEN 20
BL 60 IF LOR=1 THEN FF=8:DQ$="D:":DQ$(LEN
(DQ$)+1)=NAME$:GOTO 560
YE 70 GOTO 560:REM LINE 20 CALCULATES COM
PLEX SQUARE OPERATION, COUNTS NUMBER 0
F ITERATIONS AND, DETERMINES SIZE
DQ 80 REM LINE 30 ASSIGNES COLOR TO PIXEL
STORES COLOR, ZEROS VARIABLES AND, I
NCREMENTS COLUMN NUMBER
UW 90 REM LINE 40 PLOTS COLORS WHEN MAX N
UMBER OF COLUMNS 15 REACHED AND, INCRE
MENTS ROW NUMBER
CX 100 DIM DQ$(12),Z$(10),GR$(2),NAME$(15
),SM$(l8),DC$(10),B$(10):FOR A=1536 TO
1542:READ B:POKE A,B:NEXT A:DQ$="D:"
AH 110 DIM R$(28),X$(20)
PL 120 DIM NEXT$(18):PRINT "N":PRINT :PRI
NT " MANDELBROT SET GENERATOR":PR
INT :PRINT :TRAP 1270:REM BY JAMES GRE
YW 130 DIM Q(200),R(2007,T(200),P(200),RC
$(20),IC$(2a),S$(10),II$(10):RC$="REAL
CENTER ":IC$="IMAGINARY CENTER "
DE 140 DIM TH$(4):TH$="THE ":S$="SIZE ":I
I$="ENTER "
KZ 150 PRINT "TO COMPLETE A SAVED SCREEN
PRESS C":PRINT :PRINT "TO SEE DIRECTOR
Y PRESS D"
VH 160 PRINT :PRINT "TO SAVE SCREEN PRESS
S":PRINT :PRINT "TO VIEW SAVED SCREEN
PRESS V":PRINT
SJ 170 ? "FOR NONE OF THE ABOVE PRESS RET
URN":? :? "ENTER SCREEN MODE";:INPUT S
M$:IF SM$="S" THEN FF=8:GOTO 220
VB 180 IF SM$="V" THEN FF=4:GOTO 220
ZU 190 IF SM$="C" THEN LOR=1:SM$="V":FF=4
:GOTO 220
OD 200 IF SM$="D" THEN GOTO 1350
FQ 210 FF=0:GOTO 300
GY 220 PRINT :PRINT "INSERT DISK, PRESS R
ETURN WHEN READY";:INPUT B$
SW 240 DC$="D:":? "ENTER NAME";:INPUT NAM
E$:IF SM$="S" THEN 1350
BO 250 IF SM$="S" OR SM$="V" THEN DQ$(LEN
(DQ$)+1)=NAME$
TV 290 IF SM$="V" THEN GOTO 610
OB 300 PRINT :PRINT "FOR HIGH RESOLUTION
GRAPHICS PRESS H"
VO 310 PRINT :PRINT "FOR MEDIUM RESOLUTIO
N GRAPHICS PRESS M"
CU 320 PRINT "FOR LOW RESOLUTION GRAPHICS
PRESS L"
GL 330 PRINT :PRINT "FOR VERY LOW RESOLUT
ION PRESS V"
ST 340 PRINT :PRINT :PRINT "MAKE GRAPHICS
SELECTION";:INPUT GR$:IF Z$="0" OR B$
="I" THEN GOTO 380
KL 350 PRINT :PRINT ;II$;;RC$;;:INPUT E
RW 360 PRINT ;II$;;IC$;;:INPUT H
UL 370 PRINT ;II$;;S$;;:INPUT S:IF S<=0 T
HEN PRINT "SIZE MUST BE POSITIVE":GOTO
370
RP 380 PRINT "ENTER ITERATION LIMIT";:INP
UT IL
XP 381 PRINT :IF IL<10 THEN PRINT "ITERAT
ION LIMIT MUST BE TEN OR GREATER":GOTO
380
SV 390 REM LINES 410-450 ASSIGN SPECIC VA
LUES TO BE USED IN CALCULATIONS DEPEND
ING UPON GRAPHICS MODE
KT 400 PRINT "PLEASE WAIT, INITIALIZING V
ARIABLES"
JY 410 IF GR$="L" OR GR=21 THEN L=80:D=1.
54:Y=79:W=3:F=48:GR=21:LO=150:HI=4:GOT
O 450
CF 428 IF GR$="V" OR GR=19 THEN L=40:D=1.
54:Y=39:W=3:F=24:GR=19:LO=168:HI=1:GOT
O 450
EJ 430 IF GR$="H" OR GR=31 THEN L=160:D=0
.77:Y=159:W=3:F=170:GR=31:LO=202:HI=31
:GOTO 450
NG 440 F=170:L=80:D=0.385:Y=79:W=15:GR=11
:L0=202:HI=31
FC 450 A=S/L:M=E-S/2:N=H+S/2.6
LN 460 REM LINE 470 CALCULATES COLUMN AND
ROW VALUES FOR COLORS AND SIZE SELECT
ED IT THEN STORES THEM IN ARRAYS
EU 470 FOR G=0 TO Y:Q(G)=M+G*A:NEXT G:FOR
K=0 TO F:R(K)=N-K*A*D:NEXT K:C=0
OF 480 REM LINES 490-540 ASSIGN COLOR UAL
UES FOR SPECIFIC COUNTS
NE 490 C=C+1:B=1:VO=C:IF C=IL THEN 530
CF 500 VO=VO-1:IF VO<=1 THEN P(C)=B:GOTO
490
YP 510 IF B=W THEN B=0
QD 520 B=B+I:GOTO 500
EG 530 IF LOR=1 THEN P(C)=0:G=0:K=Kl:V=Q(
G):Z=R(K):C=0:I=0:J=0:GOTO 20
EK 540 P(C)=0:G=0:K=0:C=0:V=Q(G):Z=R(K):G
RAPHICS GR:GOTO 20
PZ 550 REM LINES 560-630 ARE I/O ROUTINES
RUN
WN 560 IF FF=0 THEN 680
XB 570 CLOSE #1:POKE 764,12:OPEN #1,8,6,D
Q$:PUT #1,GR:PRINT #1,E:PRINT #1,H:PRI
NT #1,S:PUT #1,IL
FB 580 PUT #1,HI:PUT #1,LO:PUT #1,G:PUT #
1,K
QV 590 POKE 764,12:POKE 852,PEEK(88):POKE
853,PEEK(89):POKE 856,LO:POKE 857,HI:
POKE 850,FF+3:A=USR(1536,16):CLOSE #1
QT 600 GOTO 680
JQ 610 CLOSE #1:POKE 764,12:OPEN #1,4,0,D
Q$:GET #1,GR:INPUT #1,E:INPUT #1,H:INP
UT #1,S:GET #1,IL:GET #1,HI
QZ 620 GET #1,LO:GET #1,G1:GET #1,K1:GRAP
HICS GR:SETCOLOR 4,0,2
QK 630 POKE 764,12:POKE 852,PEEK(88):POKE
853,PEEK(89):POKE 856,LO:POKE 857,HI:
POKE 850,FF+3:A=USR(1536,16):CLOSE #1
RF 640 IF LOR=1 THEN GOTO 410
RD 650 GOTO 680
JT 670 DATA 104,104,104,170,76,86,228
WG 680 SOUND 0,0,0,0
AL 690 POKE 53774,247:REM STARTS PM
HS 700 DATA 255, 129,129,129,129,129,129,
129,189,165,165,165,165,165,165,165,16
5,165,165,165
ZC 710 DATA 165,165,165,189,129,129,129,1
29,129,129,129,129,129,255
JO 720 DATA 104,160,1,177,203,136,145,203
,196,205,200,200,144,245,198,203,96,10
4,164,205,177
PU 730 DATA 203,200,145,203,136,136,16,24
7,230,203,96
ZU 740 A=PEEK(106)-48:POKE 106,A:POKE 542
79,A:ST=256*A:POKE 559,62:POKE 53277,3
:POKE 53256,3
HU 750 FOR I=ST+1024 TO ST+1280:POKE I,0:
NEXT I:PST=ST+1025:POKE 204,INT(PST/25
6):POKE 203,PST-(PEEK(204)*256)-1
IC 760 POKE 205,34:RESTORE 700:FOR I=PST
TO PST+33:READ A:POKE I,A:NEXT I:FOR I
=1550 TO 1581:READ J:POKE I,J:NEXT I
PL 770 FOR Z=1 TO 30:GOSUS 890:NEXT Z:I=3
8:POKE 764,7:VR=5
VI 780 CU=PEEK(764):REM LINES 780-930 ARE
FOR CURSOR MOVEMENT 930, IS END OF P
M
TD 790 IF CU=7 THEN I=I+10:POKE 53248,I:I
F I>=240 THEN I=10
TS 800 IF CU=135 THEN I=I+I:POKE 53248,1:
IF I>=240 THEN I=10
FL 810 IF CU=6 THEN I=I-10:POKE 53248,I:I
F I<=10 THEN I=200
GP 820 IF CU=134 THEN I=I-1:POKE 53248,I:
IF I<=10 THEN I=200
MP 830 IF CU=14 THEN FOR GG=1 TO 20:GOSUB
910:NEXT GG
KH 840 IF CU=142 THEN GOSUB 910
YH 850 IF CU=15 THEN FOR GG=1 TO 20:GOSUB
890:NEXT GG
SG 860 IF CU=143 THEN GOSUB 890
CC 870 IF CU=12 THEN POKE 559,0:GOTO 938
YO 880 POKE 764,32:GOTO 780
HQ 890 IF VR>=180 THEN RETURN
NW 900 VR=VR+1:A=USR(1567):POKE 704,280:R
ETURN
BL 910 IF VR<=-20 THEN RETURN
IB 920 VR=VR-1:A=USR(1550):POKE 704,200:R
ETURN
YV 930 POKE 53248,0:POKE 106,PEEK(106)+48
:REM FOLLOWING LINES DET. COORDS AND S
TARTING OF ANOTHER SET
KE 940 IF GR=11 THEN G=INT(I/2)-16:K=VR+1
2:JJ=1:D=0.385:L=80
UX 950 IF GR=19 THEN G=INT(((I/2)-16)/2):
K=INT((VR/4+2)/2):JJ=0.42:D=1.54:L=40
GD 960 IF GR=21 THEN G=INT(I/2)-16:K=VR/4
+2:JJ=1:D=1.54:L=80
EA 970 IF GR=31 THEN G=2*(INT(I/2)-22)+12
:K=VR+12:JJ=2:D=0.77:L=160
FN 980 A=S/L:M=E-S/2:N=H+S/2.6
HT 990 E=M+G*A:H=N-K*A*D
MO 1000 PRINT "
 ":PRINT "THE REAL
CENTER
":PRINT "THE REAL
CENTER OF THE CURSOR IS ";E
WE 1010 PRINT :PRINT "THE IMAGINARY CENTE
R IS ";H
IY 1020 PRINT :PRINT "THE SIZE OF THE INN
ER CURSOR IS ";:SI=5*A*JJ:PRINT SI
YO 1030 PRINT :PRINT "THE SIZE OF THE OUT
ER CURSOR IS ";:SO=12*A*JJ:PRINT SO
RM 1040 PRINT :PRINT "DO YOU WANT TO CREA
TE A NEW SET Y OR N";:POKE 764,28:INPU
T Z$
RK 1050 IF Z$="Y" THEN GOTO 1150
PR 1060 GOTO 1230
AL 1070 PRINT "WHICH PARAMETER(S) DO YOU
WISH TO CHANGE R, I, S":INPUT Z$
JV 1080 IF Z$="R" THEN PRINT ;II$;;RC$;;:
INPUT E:GOTO 1120
ZF 1090 IF Z$="I" THEN PRINT ;II$;;IC$;;:
INPUT H:GOTO 1120
GG 1100 IF Z$="S" THEN PRINT ;II$;;S$;;:I
NPUT S:IF S<=0 THEN PRINT "SIZE MUST B
E GREATER THAN ZERO":GOTO 1100
OF 1110 GOTO 1120
AN 1120 PRINT ;TH$;;RC$;;E;:PRINT :PRINT
:PRINT ;TH$;;IC$;;H;:PRINT :PRINT :PRI
NT ;TH$;S$;;S;
IS 1121 PRINT :PRINT :PRINT "DO YOU WISH
TO CHANGE ANY MORE Y OR N";:INPUT B$
KB 1130 IF B$="Y" THEN GOTO 1070
ON 1140 GOTO 1210
FX 1150 PRINT :PRINT :PRINT "SELECT SIZE
VALUE:":PRINT
OE 1160 PRINT "INNER CURSORS SIZE VALUE":
PRINT :PRINT "OUTER CURSORS SIZE VALUE
"
FC 1161 PRINT :PRINT "YOUR OWN SIZE":PRIN
T :PRINT :PRINT "SELECT I, O OR S";
UB 1170 INPUT B$:IF B$="S" THEN Z$="S":GO
TO 1100
KC 1180 IF B$="O" THEN S=SO:GOTO 1120
BR 1190 IF B$="I" THEN S=SI:GOTO 1120
NE 1200 GOTO 1100
EK 1210 Z$="O":PRINT "TO SAVE SCREEN PRES
S S OTHERWISE RETURN":INPUT SM$:I
F SM$="S" THEN FF=8:GOTO 220
TT 1220 FF=0:B$="0":GRAPHICS 11:GOTO 300
RS 1230 PRINT :PRINT "DO YOU WANT TO QUIT
, GO BACK TO SELECTED VALUES, OR
START A NEW SET Q, G, OR S";
OP 1231 INPUT Z$
UQ 1240 IF Z$="Q" THEN END
EE 1250 IF Z$="S" THEN CLR :GOTO 10
NK 1260 GOTO 1000
KC 1265 REM LINES 1270-1330 ARE ERROR HAN
DLING/DETECTING ROUTINES
ND 1270 LINERR=PEEK(187)*256+PEEK(186):ER
R=PEEK(195):TRAP 40000:TRAP 1270
XM 1275 IF ERR=165 THEN ? "BAD FILE NAME,
TRY AGAIN":POKE 764,28:GOTO 240
DI 1280 IF ERR=139 OR ERR=140 OR ERR=142
OR ERR=143 OR ERR=163 OR ERR=136 THEN
PRINT "I/O ERROR":END
SW 1285 IF ERR=138 OR ERR=144 THEN GOTO L
INNER
EX 1290 IF ERR=145 OR ERR=160 THEN PRINT
"DISK ERROR":END
QH 1300 IF ERR=170 THEN PRINT "FILE NOT O
N DISK, TRY AGAIN":POKE 764,28:DQS="D:
":GOTO 240
MD 1310 IF ERR=8 THEN FOR AA=1 TO 50:SOUN
D 0,100,10,15:NEXT AA
EQ 1320 SOUND 0,0,0,0:PRINT :PRINT "*****
*REENTER******":PRINT :GOTO LINERR
XY 1330 PRINT "ERROR NUMBER ";ERR;" AT LI
NE ";LINERR;:END
WU 1340 REM LINES 1350-1400 ARE USED WITH
I/O ROUTINES ABOVE
PK 1350 CLOSE #4:OPEN #4,6,0,"D:*.*":IF S
M$<>"S" THEN GOTO 1390
HH 1360 INPUT #4,R$:TRAP 1400:X$=R$(3,LEN
(NAME$)+2):IF X$<>NAME$ THEN IF R$(10,
16)<>"SECTORS" THEN GOTO 1360
RB 1370 IF X$=NAME$ THEN PRINT "NAME ALRE
ADY USED ON DISK, TRY AGAIN":TRAP 4000
0:TRAP 1270:GOTO 240
TG 1380 TRAP 40000:TRAP 1270:GOTO 250
OF 1390 INPUT #4,R$:TRAP 1400:PRINT R$:IF
R$(10,16)<>"SECTORS" THEN 1390
OE 1400 CLOSE #4