The Magic Of Tesselations
-Part II
by Allan Moose and Marian Lorenz
The theme of distorting a basic tile shape as it is drawn in successive rows forms the basic idea behind many of M.C. Escher's drawings,
A tesselation or tiling is the complete covering of a flat surface by one or more figures in a pattern, with no overlapping of the figures and no open spaces. As we discussed last month, tesselations are commmonly found in linoleum patterns, parquet floors or fabrics.
All of the tilings we discussed, and many of the tilings found around one's home, share the property of being periodic. A tesselation is periodic if you can shift the drawing without rotation or reflection to a new position where all outlines again fit exactly. While there are an infinite number of shapes that will tesselate periodically, periodic tilings by no means exhaust all of the possible ways to cover a plane surface. In this article we will present two programs that illustrate more intricate tilings. The first draws a non-periodic tiling that has rotational symmetry. The second covers the screen with tiles that are gradually deformed as each successive row is drawn on the screen.
One of the charming things about the study of tilings is that it bridges the gap between art and science. Mathematicians have related tilings to group theory, which is the abstract study of symmetry. Physicists study tesselations to gain insights into the formation of crystals, and, of course, the famous artist M. C. Escher made frequent use of tilings in his work. In developing our programs we drew upon ideas from all of these fields. In particular, we have made use of the ideas of translation and rotation of coordinates as a way of writing short programs that you may easily modify.
In order to illustrate tesselations with rotational symmetry, the basic tile used is a diamond which is based on a 30-60-degree right triangle.
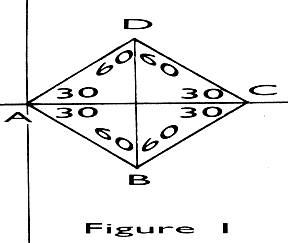
Previously, we introduced the use of a "local coordinate system" (LCS). The idea behind a LCS is that if you want to repeatedly draw the same figure on the CRT screen, the most efficient way to do it is to represent the coordinates o£ the vertices of the figure (points A,B,C,D in Figure 1) in terms of a hypothetical coordinate system. Then to draw the figure on the screen all you do is position the origin of the LCS where you want it and draw. In this way, the same subroutine can draw all the tiles you need.
In the LCS, the coordinates of the vertices of Figure 1 are:
A = 0, 0
B = 17.32, -10
C = 34.64, 0
D = 17.32, 10
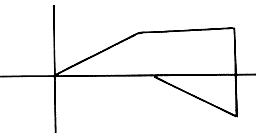
To make a tesselation with rotational symmetry, we want to draw this diamond in a circular pattern so that the first row will look like:
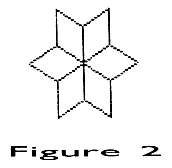
The next circular row must fit around this design. The algorithm for generating the pattern can be simply stated as:
READ, ROTATE, TRANSLATE.
That is, for each diamond, no matter where it is, the program first reads the data numbers, then rotates the figure into the proper position, and then translates the vertex of the diamond to the proper location.
With this background, you should be able to follow the program of Listing 1. This program creates three rows of diamonds (Figure 3). You may easily modify it to add a fourth. Be sure to include a clipping routine to avoid the dreaded "cursor out of range" error!
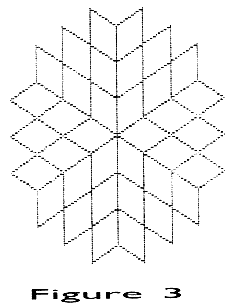
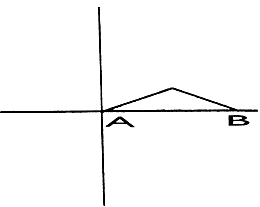
Of course, you will want to experiment with more than just diamond tiles. An excellent place to start is with triangle tilings. The reason is that each tile can be changed by distorting the legs. For example, change
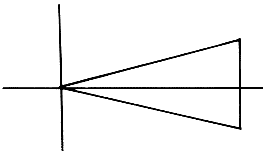
to
by nending each leg from
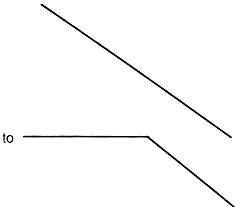
Actually you can be more imaginative than this because a triangle can be distorted in an infinite number of ways to yield a figure capable of being used in a rotational tesselation.
The theme of distorting a basic tile shape as it is drawn in successive rows forms the basic idea behind many of M. C. Escher's drawings. For example, birds might gradually lose their shapes and become checkerboarded fields of hay or even metamorphose completely into fish as in "Sky and Water 1." Our second program illustrates this gradual metamorphosis of one shape into another. In addition to being indebted to M. C. Escher for inspiration, we also must credit Douglas Hofstadter who, several years ago, devoted a column of "Metamagical Themas" in Scientific American to "Parquet Deformations."
The basic idea is that simple geometric shapes which can tile the plane are slowly deformed as they move across or down the plane. Deformations may be created with a number of simple techniques such as:
1. Lengthening or shortening a line.
2. Introducing a "hinge" into a line segment so that it can flex.
3. Rotating a line or a group of lines that form a natural sub-unit.
4. Introducing a small "bump" or tooth into a line segment.
By using one of these techniques and allowing it to continue long enough, such deformations can have unexpected results; one outcome being that tiles at the end of the work bear little or no resemblance to those at the beginning.
In order to keep our program simple, we restricted it to drawing a diamond and flexing the sides of the tile "in" or "out" to deform it. There are, of course, many other methods of deforming tiles, just as there are many other shapes that lend themselves to deformation. Here is a chance to exercise your creativity by building upon the ideas in this program.
It is evident that drawing a tesselation in which the shape of the tile is changed before each row is drawn is more involved than simply drawing the same tile many times. We have approached this problem by introducing what at first
Physicists study tesselations to
gain insights into the formation of
crystals,
glance may seem like an unnecessary complication. First, we note that many shapes which can tile a surface have some sort of rotational symmetry. This means that if you rotate the shape around its center through some fraction of a circle (1/2, 1/3, 1/6, etc.) you get back the original shape. If this is the case, and it certainly is with the diamond, then we need only specify part of the shape, say two sides, and let the computer rotate that part as often as necessary to close the shape. You should visualize this rotation as taking place in the LCS. The rotation routine necessary to do this is the same as the rotation subroutine in Listing 1, lines 140 and 150. If we must rotate the part of the shape N times to produce a closed figure, then the angles through which we must rotate it are multiples o£ 360/N. Having constructed the tile in a LCS, it may be easily translated to the proper positions and plotted on the screen.
Introducing the extra step of putting a tile together by rotation gives us a way to deform the tiles. Conceptually, deforming a tile is rather simple. Just take each side of the tile in turn, keeping the end points stationary, move the midpoint alternately in toward the center or out away from the center one unit at a time. The problem is in determining where to move the midpoint to. That is, given the coordinates of the end points, what are the coordinates of the point one, two, or three units closer to, or farther from the tile's center than the line's midpoint? If the line happens to be horizontal or vertical, then there is no problem. For example, a horizontal line's midpoint has the same ycoordinate as its end points. It has an x-coordinate equal to the average of the x-coordinates of the ends. Moving the midpoint toward or away from the center is a matter of moving it up or down. That is, the x-coordinate stays the same and the y-coordinate increases or decreases by one. If the line is diagonal we can still find the midpoint easily enough. However, moving it is the hard part, as the distance and direction of movement depend entirely on the inclination of the line segment.
It would be much easier for the purposes of this exercise if we could make each side horizontal long enough to deform it and then put it back where it belongs. Fortunately, we already have the tools available to do just that-local coordinates and rotation. In mathematical terms we want to:
• Translate each line segment to the origin.
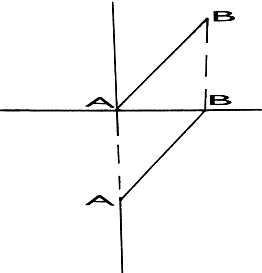
• Rotate it onto positive x-axis,
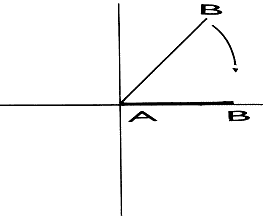
• Deform it as explained above.
• Rotate and translate it back into position.
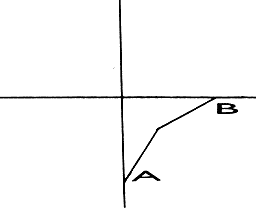
For us the procedure is as follows:
1. Take each of the defined sides in turn. Pick one end point and call it X1, Y1. Call the other end X2, Y2.
2. If we shift the origin of the LCS to the point at X1, Y1 then the other point will have the coordinates (X2-X1), (Y2-Y1).
3. Find the inclination of the line or the angle theta which it makes with the xaxis. If the line is vertical, then THETA = 90. If the line slopes towards the right (x2 > x1), then THETA= ARCTAN ((Y2-Y1)/(X2-X1)). If the line slopes towards the left (X2<X1), then THETA = 180 +ARCTAN((Y2-Y1)/(X2-XI)).
4. Rotate both end points, in terms of their coordinates relative to the first point, through this angle. The point 0,0 will not move, of course, but the other point should now have a y-coordinate of 0, meaning the line is now lying horizontally on the x-axis.
5. Finding and deforming the midpoint is now trivial. Its x-coordinate will be half the length and its y-coordinate plus or minus 1, 2, 3, etc.
6. Now all we need do is move the deformed line back where it belongs. This is just a matter of rotating through an angle Theta and then adding X1, Y1 to the coordinates of each point.
A moment's consideration will convince you that we will get back the original coordinates of our line plus the rotated and translated coordinates of the midpoint. By design, we will make all of these calculations once. Only for the sides of the tiles which are actually defined and only for the first tile of a row. The remainder of the first tile and all the other tiles in that row are derived from the defined sides by rotation and shifting as usual.
The program in Listing 2 differs from our previous tiling programs by keep ing the coordinate values of the vertices in an array. Two arrays are maintained. The first stores the original vertex coordinates. The second, larger one, holds the coordinates of the deformed tile.
The data necessary for drawing the tiles is given in lines 140 and 150. This means that to change the shape of your basic tile you need only change one or two program lines. In fact, it turns out that you don't have to change the tile shape in order to change the design drawn by the computer. Try specifying the diamond tile by two vertices and four rotations:
140 DATA 2, 4
150 DATA 0, -8, 8, 0
150 DATA 0, -8, 8, 0
rather than by three vertices and two rotations. When the number of vertices is odd, line 850 will flex the sides alternately "in" or "out." When the number of vertices specified is even, all sides will be flexed "in."
It is evident that changing the tiling produced by the second program is a simple task. Because of this the program is great for experimentation! Some suggestions are to try square, rectangular, or hexagonal tiles and change the type of deformations used.
Tesselations
Listing 1.
Basic
DX 10 REM ROTATIONAL TESSELATION
NV 20 REM BY ALLAN MOOSE AND MARIAN LOREN
Z
BB 40 REM
JN 50 REM **** INITIALIZE SYSTEM ****
BD 60 REM
RX 70 GRAPHICS 24:COLOR 1
CS 80 DEG :A=0:B=0
OI 90 DATA 0,0,17.32,-10,34.64,0,17.32,10
,0,0
ON 100 GOTO 450
QO 110 REM
PJ 120 REM **** ROTATION SUBROUTINE ****
QS 130 REM
AH 140 XPRIME=X*COS(THETA)-Y*SIN(THETA)
WF 150 YPRIME=X*SIN(THETA)+Y*COS(THETA)
IG 160 SCRNX=160+XPRIME
VX 170 SCRNY=96-YPRIME
ZN 180 RETURN
WM 200 REM **** END ROTATION SUBROUTINE *
***
QP 210 REM
QJ 220 REM **** SET TRANSLATION DISTANCES
FOR SECOND ROW ****
UK 230 A=17.32:B=10:RETURN
OT 240 A=0:B=20.32:RETURN
WJ 250 A=-17.32:B=10:RETURN
WO 260 A=-17.32:B=-10:RETURN
MD 270 A=0:B=-20.32:RETURN
TR 280 A=17.32:B=-10:RETURN
ET 290 REM **** SET TRANSLATION DISTANCES
FOR THIRD ROW ****
XN 300 A=34.64:B=0:RETURN
WZ 310 A=34.64:B=20:RETURN
WA 320 A=17.32:B=30:RETURN
EE 330 A=0:B=40:RETURN
XO 340 A=-17.32:B=30:RETURN
YU 350 A=-34.64:B=20:RETURN
XO 360 A=-34.64:B=0:RETURN
ZC 370 A=-34.64:B=-20:RETURN
YB 380 A=-17.32:B=-30:RETURN
WF 390 A=0:B=-40:RETURN
UJ 400 A=17.32:B=-30:RETURN
VL 410 A=34.64:B=-20:RETURN
QT 420 REM
CF 430 REM **** PLOT THE FIRST ROW ****
QX 440 REM
VY 450 FOR THETA=0 TO 360 STEP 60
US 460 READ X,Y:GOSUB 140:PLOT SCRNX,SCRN
Y
QI 470 READ X,Y:GOSUB 140:DRAWTO SCRNX,SC
RNY
QK 480 READ X,Y:GOSUB 140:DRAWTO SCRNX,SC
RNY
QM 490 READ X,Y:GOSUB 140:DRAWTO SCRNX,SC
RNY
PV 500 READ X,Y:GOSUB 140:DRAWTO SCRNX,SC
RNY
TJ 510 RESTORE 90
TN 520 NEXT THETA
OW 530 REM
ZE 540 REM **** PLOT THE SECOND ROW ****
RA 550 REM
WB 560 FOR THETA=0 TO 360 STEP 60
MS 570 FOR J=1 TO 2
QU 580 I=I+1
CA 590 ON I GOSUB 280,230,230,240,240,250
,250,260,260,270,270,280
TI 680 RESTORE 90
QB 610 READ X,Y:GOSUB 140:PLOT SCRNX+A,SC
RNY-B
CN 620 READ X,Y:GOSUB 140:DRAWTO SCRNX+A,
SCRNY-B
CP 630 READ X,Y:GOSUB 140:DRAWTO SCRNX+A,
SCRNY-B
CR 640 READ X,Y:GOSUB 140:DRAWTO SCRNX+A,
SCRNY-B
CT 650 READ X,Y:GOSUB 140:DRAWTO SCRNX+A,
SCRNY-B
GS 660 NEXT J
TY 670 NEXT THETA
FX 680 I=0
RJ 690 REM
NH 700 REM **** PLOT THE THIRD ROW ****
QU 710 REM
VV 720 FOR THETA=0 TO 360 STEP 60
NC 730 FOR J=1 TO 3
QO 740 I=I+1
QE 750 ON I GOSUB 410,300,310,310,320,330
,330,340,350,350,360,370,370,380,390,3
90,400,410
TV 760 RESTORE 90
QO 770 READ X,Y:GOSUB 140:PLOT SCRNX+A,SC
RNY-B
DA 780 READ X,Y:GOSUB 140:DRAWTO SCRNX+A,
SCRNY-B
DC 790 READ X,Y:GOSUB 140:DRAWTO SCRNX+A,
SCRNY-B
CL 800 READ X,Y:GOSUB 140:DRAWTO SCRNX+A,
SCRNY-B
CN 810 READ X,Y:GOSUB 140:DRAWTO SCRNX+A,
SCRNY-B
CN 820 NEXT J
TS 830 NEXT THETA
RB 840 REM
MK 850 REM **** SCREEN DUMP ****
RF 860 REM
MZ 870 DIM GRAF$(200)
RS 875 GOSUB 1000
AC 880 GRAF$(1)=CHR$(0):GRAF$(200)=CHR$(0
):GRAF$(2)=GRAF$
MO 890 LPRINT CHR$(27);CHR$(65);CHR$(8)
GR 900 SCRNMEM=PEEK(88)+PEEK(89)*256
LU 910 MEMLOC=SCRNMEM+40*191
TF 920 HIBYTE=INT(ADR(GRAF$)/256)
EW 930 LOBYTE=ADR(GRAF$)-HIBYTE*256
EP 940 POKE 203,LOBYTE:POKE 204,HIBYTE
AQ 950 FOR SCRNCOL=MEMLOC TO MEMLOC+39
CL 960 DUMP=USR(1536,SCRNCOL)
EH 970 LPRINT CHR$(27);CHR$(75);CHR$(200)
;CHR$(0);GRAF$
KB 980 NEXT SCRNCOL
OQ 990 END
JE 1000 RESTORE 1040
HD 1010 FOR K=0 TO 43
BY 1020 READ ML:POKE 1536+K,ML
FU 1030 NEXT K
NZ 1040 DATA 104,104,141,15,6,104,141,14,\
6,160,4,162,192,173,0,0,202,240,24
EF 1050 DATA 145,203,200,216,173,14,6,56,
233,40,141,14,6
ZX 1060 DATA 144,3,76,13,6,206,15,6,76,13
,6,96
AU 1070 RETURN
Listing 2.
Basic
SS 10 REM **** ESCHER VERSION 5 ****
NV 20 REM BY ALLAN MOOSE AND MARIAN LOREN
Z
BB 40 REM
NI 50 GOTO 140
FW 60 REM **** ROTATION SUBROUTINE ****
BE 70 REM
MN 80 XPRIME=X*COS(THETA)-Y*SIN(THETA)
IL 90 YPRIME=X*SIN(THETA)+Y*COS(THETA)
YX 100 RETURN
QO 110 REM
XK 120 REM **** INITIALIZE SYSTEM, VARIAB
LES, ARRAYS ****
QS 130 REM
DL 140 DATA 3,2
BD 150 DATA 0,-8,8,0,0,8
NT 160 GRAPHICS 24:DEG :COLOR 1
IJ 170 READ NUMVERTS,NUMROTS
NP 180 DIM ARRAY1(NUMVERTS,2),ARRAY2(NUMV
ERTS*2-1,2)
LE 190 THETAINC=360/NUMROTS
HN 200 FOR VERTEX=1 TO NUMVERTS
QV 210 READ XCOORD,YCOORD
IV 220 ARRAY1(VERTEX,1)=XCOORD:ARRAY1(VER
TEX,2)=YCOORD
ZX 230 NEXT VERTEX
SP 240 REM **** DETERMINE HEIGHT AND WIDT
H OF TILE ****
HX 250 FOR VERTEX=1 TO NUMVERTS
CD 260 IF ABS(ARRAY1(VERTEX,1))>XMAX THEN
XMAX=ABS(ARRAY1(VERTEX,1))
II 270 IF ABS(ARRAY1(VERTEX,2))>YMAX THEN
YMAX=ABS(ARRAY1(VERTEX,2))
AH 280 NEXT VERTEX
BJ 290 HEIGHT=2*YMAX:WIDTH=2*XMAX
SI 300 MAXCOLS=INT(320/WIDTH)-1
UJ 310 MAXROWS=INT(192/HEIGHT)-1
SR 320 INITIALX=XMAX+5:INITIALY=YMAX+5
QU 330 REM
YF 340 REM **** PLOT THE FIRST ROW OF TIL
ES ****
QY 350 REM
HD 360 FOR COL=1 TO MAXCOLS
UP 370 FOR THETA=0 TO 360 STEP THETAINC
IE 380 FOR VERTEX=1 TO NUMVERTS
ZU 390 X=ARRAY1(VERTEX,1):Y=ARRAY1(VERTEX
,2)
VO 400 GOSUB 80
LV 410 SCRNX=INITIALX+(COL-1)*WIDTH+XPRIM
E
RM 420 SCRNY=INITIALY-YPRIME
KH 430 IF VERTEX=1 THEN PLOT SCRNX,SCRNY:
GOTO 450
PL 440 DRAWTO SCRNX,SCRNY
AD 450 NEXT VERTEX
TU 460 NEXT THETA
UN 470 NEXT COL
RF 480 REM
LY 490 REM **** DRAW SUCCEEDING ROWS OF T
ILES ****
QQ 500 REM
NA 510 FOR ROW=2 TO MAXROWS
TQ 520 YOFFSET=YOFFSET+1
UU 530 GOSUB 730
HB 540 FOR COL=1 TO MAXCOLS
UN 550 FOR THETA=0 TO 360 STEP THETAINC
SP 560 FOR VERTEX=1 TO NUMVERTS*2-1
BJ 570 X=ARRAY2(VERTEX,1):Y=ARRAY2(VERTEX
,2)
WF 580 GOSUB 80
MM 590 SCRNX=INITIALX+(COL-1)*WIDTH+XPRIM
E
EQ 600 SCRNY=INITIALY+(ROW-1)*HEIGHT-YPRI
ME
PI 610 IF VERTEX=1 THEN PLOT SCRNX,SCRNY:
GOTO 660
YA 620 REM CLIPPING ROUTINE
KP 630 IF SCRNX<0 OR SCRNX>319 THEN GOTO
940
JU 640 IF SCRNY<0 OR SCRNY>191 THEN GOTO
940
PP 650 DRAWTO SCRNX,SCRNY
AH 660 NEXT VERTEX
TY 670 NEXT THETA
UR 680 NEXT COL
FP 690 NEXT ROW
QG 700 GOTO 940
QU 710 REM
GL 720 REM **** SUBROUTINE TO CREATE AN A
RRAY OF DEFORMED TILES ****
QY 730 REM
HQ 740 FOR I=1 TO NUMVERTS-1
TP 750 X1=ARRAY1(I,1):ARRAY2(2*I-1,1)=ARR
AY1(I,1)
MP 760 X2=ARRAY1(I+l,1)
XP 770 Y1=ARRAY1(I,2):ARRAY2(2*I-1,2)=ARR
AY1(I,2)
NR 780 Y2=ARRAY1(I+1,2)
CH 790 X=X2-X1:Y=Y2-Y1
UE 800 IF X=0 THEN THETA=(-1)*SGN(Y)*98:G
OTO 850
QO 810 THETA=ATN(Y/X)
OA 828 IF X<0 THEN THETA=180+THETA
FM 830 THETA=-THETA:REM ROTATE TOWARD X-A
XIS
WA 840 GOSUB 80
XL 850 X=XPRIME/2:Y=YOFFSET*(-1)^(I+1)
LX 860 THETA=-THETA:REM ROTATE BACK INTO
POSITION
WG 870 GOSUB 80
FD 880 ARRAY2(2*I,1)=XPRIME+X1:ARRAY2(2*I
,2)=YPRIME+Y1
GO 890 NEXT I
IV 900 REM **** COMPLETE ARRAY2 ****
SU 910 FOR J=1 TO 2:ARRAY2(2*NUMVERTS-1,J
)=ARRAY1(NUMVERTS,J):NEXT J
ZJ 920 RETURN
MH 930 REM **** SCREEN DUMP ****
UY 940 GOSUB 1080
MW 950 DIM GRAF$(200)
ZZ 960 GRAF$(1)=CHR$(0):GRAF$(200)=CHR$(0
):GRAF$(2)=GRAF$
ML 970 LPRINT CHR$(27);CHR$(65);CHR$(8)
HH 980 SCRNMEM=PEEK(88)+PEEK(89)*256
MK 990 MEMLOC=SCRNMEM+40*191
MZ 1000 HIBYTE=INT(ADR(GRAF$)/256)
FW 1010 LOBYTE=ADR(GRAF$)-HIBYTE*256
MY 1020 POKE 203,LOBYTE:POKE 204,HIBYTE
MP 1030 FOR SCRNCOL=MEMLOC TO MEMLOC+39
PW 1040 DUMP=USR(1536,SCRNCOL)
RG 1050 LPRINT CHR$(27);CHR$(75);CHR$(200
):CHR$(0);GRAF$
AK 1060 NEXT SCRNCOL
FI 1070 END
JL 1080 RESTORE 1120
IB 1090 FOR K=0 TO 43
BU 1100 READ ML:POKE 1536+K,ML
FO 1110 NEXT K
NV 1120 DATA 104,104,141,15,6,104,141,14,
6,160,4,162,192,173,0,0,202,240,24
EB 1130 DATA 145,203,200,216,173,14,6,56,
233,40,141,14,6
ZT 1140 DATA 144,3,76,13,6,206,15,6,76,13
,6,96
AQ 1150 RETURN