Matrix Row Operations
A mathematics classroom-teaching aid
William L. Hinrichs
Rockford, III.
After teaching the elementary row operations on matrices and their applications on a chalkboard or overhead projector for many years, I have found a better teaching tool. Using a computer and this program, Matrix Row Operations, has eliminated a major stumbling block to learning. Detailed fraction arithmetic always obscured the big picture concepts and techniques. All of the input and output for this program is in the common fraction form used in textbooks and familiar to the students. However, all fraction arithmetic including multiplication, addition, and reducing is done by the computer. This allows us to concentrate on the big picture while avoiding the details during classtime.
Easy Conversion For Apple & TRX-80
This program was written for a Commodore PET computer, but with minor modifications it will run on an Apple, TRS-80, or other machine. No machine language is used and the BASIC used is standard. Due to a lack of standardization of screen control statements, most of the PRINT statements will have to be modified. Loop index variables have been left off some NEXT statements and may have to be added.
Classroom Equipment Set-up
All that is required to use this program with a small group is a PET computer with 8-K RAM and any ROM version. Due to the array size limitation of version 1.0, the program's use is limited but it will run and can be used effectively. For a large group, I use a Petunia video interface board from HUH Electronics to connect our PET to a TV monitor and then connect that monitor to a second monitor with very satisfactory results. This arrangement has worked well with up to 40 students in a class.
Sample Run
Before I describe the program, a sample run is in order. We will solve a system of two equations in two unknowns by matrix row reduction.
Problem:
Find all solutions, if any, of this system of linear equations:
5x + 3y = 9 and -4x + 2y = -16.
Mathematical Analysis
We will set up a matrix representation of this system of equations and manipulate it by applying the elementary row operations. At each step, we will have a matrix representation of a system of equations with the same solutions as the original one. Our goal is to end up with a matrix representation in row-reduced form, from which the solution to all the systems can be easily read. The original and row-reduced matrices are illustrated in the computer solution below. For more information on the mathematics of matrices, I would recommend College Algebra, Gustafson & Frisk, Brooks/Cole Pub. Co., 1980, pp. 116-175. Most other college algebra texts also have a chapter on matrices.
Computer Demonstration
- LOAD the program and RUN it.
The displays which follow are exact copies of the screen. Each display has had all inputs added to the right of the ?, and when the RETURN key is pressed we go on to the next screen. COMMAND? is always the first input requested on each screen. For some commands, additional inputs are requested above the COMMAND? line.
- The command menu will be displayed and our response to COMMAND? is 'EM' for enter matrix.
************************************ * * * COMMAND MENU * * * * ? DISPLAY MENU * * EM ENTER MATRIX * * *R MULTIPLY ROW * * *R+ MULTIPLY ROW AND ADD * * IR INTERCHANGE ROWS * * DOM DISPLAY ORIGINAL MATRIX * * DIM DISPLAY CURRENT - 1 MATRIX * * DCM DISPLAY CURRENT MATRIX * * B BACKUP 1 STEP * * Q QUIT * * * * COMMAND? EM * * * ************************************
- We can now enter our matrix row by row. In response to the prompt, we follow each entry by pressing the RETURN key. The number of rows is 2 and the number of columns is 3. We follow these responses with the matrix values by row. The COMMAND? response now is ‘DOM’ which causes the original matrix to be displayed in row, column form.
******************************* * * * HOW MANY ROWS? 2 * * HOW MANY COLUMNS? 3 * * M( 1, 1 ) = ? 5 * * M( 1, 2 ) = ? 3 * * M( 1, 3 ) = ? 9 * * M( 2, 1 ) = ? -4 * * M( 2, 2 ) = ? 2 * * M( 2, 3 ) = ? -16 * * * * * * * * * * * * COMMAND ? DOM * *******************************
- We need a 1 in the first row, first column so our COMMAND? is *R for multiply a row. We are then prompted to enter ROW TO BE MULTIPLIED?, to which we reply 1. Next we enter 1/5 to the prompt MULTIPLIER?. Note that the entry is a common fraction. Following the last entry the screen clears and the new or current matrix is displayed with all fractions reduced.
*********************************** * * * * * 5 3 9 * * * * * * * * -4 2 -16 * * * * * * * * * * * * ROW TO BE MULTIPLIED? 1 * * MULTIPLIER? 1/5 * * COMMAND? *R * * * ***********************************
- We now need a 0 in the second row, first column so our COMMAND? is *R + for multiply a row and add to another row. We answer ROW TO BE MULTIPLIED? with a 1, MULTIPLIER? with a 4, and ROW TO BE ADDED TO? with a 2. Those operations are performed and the result is displayed.
************************************ * * * 3 9 * * 1 --- --- * * 5 5 * * * * * * -4 2 -16 * * * * * * * * ROW TO BE MULTIPLIED? 1 * * MULTIPLIER? 4 * * ROW TO BE ADDED TO? 2 * * * * COMMAND? *R + * * * ************************************
- We now get a 1 in the second row, second column by responding with *R for COMMAND?, 2 for ROW TO BE MULTIPLIED?, and 5/22 for MULTIPLIER?.
************************************ * * * 3 9 * * 1 --- --- * * 5 5 * * * * 0 22 -44 * * --- --- * * 5 5 * * * * * * * * * * ROW TO BE MULTIPLIED? 2 * * MULTIPLIER? 5/22 * * COMMAND? *R * * * ************************************
- Our last row operation creates a 0 in the first row, second column by responding a COMMAND? with *R +, ROW TO BE MULTIPLIED? by 2, MULTIPLIER? by -3/5, and ROW TO BE ADDED TO? by 1. The final or row-reduced matrix will then be displayed.
************************************ * * * 3 9 * * 1 --- --- * * 5 5 * * * * * * 0 1 -2 * * * * * * * * ROW TO BE MULTIPLIED? 2 * * MULTIPLIER? -3/5 * * ROW TO BE ADDED TO? 1 * * * * COMMAND? *R+ * * * ************************************
- We now interpret this row reduced matrix as a system of equations with the same solution as the original system
x = 3 and y = - 2. ************************************ * * * * * 1 0 3 * * * * * * * * 0 1 -2 * * * * * * * * * * * * * * * * COMMAND? Q * * * ************************************
- Our last COMMAND? is Q for quit. This allows a clean exit from the program.
In class, we can handle systems of 5, 6, or more equations with no more difficulty than solving two on the chalkboard. The example was kept small to conserve space in the article. Please note that the input concerned strategy decisions involved in the row-reduction method and not with the details of the matrix row operations. Another nice command in the menu is B for backup one step. If we don't get the desired results at any step, B returns us to the status prior to the last command. At any step, we may display the original, current, or current-1 matrix. If an interchange of rows is desired the command IR causes it to happen.
Mathematics Topics Taught
I have found this program useful in teaching the strategies and application of row-reduction to solve systems of linear equations, finding the inverse of any square matrix that has one, and finding the value of a determinant of a square matrix by first zeroing all entries under the diagonal and then finding the product of the diagonal entries. Discussion of the algebra of the simplex method is clarified and simplified when using this program. The simplex method is a matrix technique for the solution of linear programming problems.
Non-Classroom Uses
Students can use this program on a PET in a learning center or library to practice and reinforce their understanding of matrix strategies. I have also found the program valuable for producing step by step handouts to supplement the examples contained in our textbook. I have been aided greatly in this last application by the KEYPRINT program written by Charles Brannon, COMPUTE! #7, pp. 84, 86. I LOAD and initialize KEYPRINT first, then whenever I want a copy of the current screen contents I proceed as usual.
Structure Of The Program
The program is a menu driven set of ten subroutines referenced from the main program by one of the menu commands. Their locations and functions are:
| COMMAND | LOCATION | FUNCTION |
| ? | 2200-2310 | Displays menu. |
| *R | 1900-1996 | Multiplies row. |
| *R + | 1700-1880 | Multiplies entries of one row and adds to another. |
| IR | 2000-2090 | Interchanges any two rows. |
| B | 2400-2430 | Backs up 1 step. Current and current-1, matrices are switches. |
| DOM | 1205-1310 | Displays original matrix. |
| DIM | 1210-1310 | Displays intermediate (current-1) matrix. |
| DCM | 1215-1310 | Displays current matrix. |
| EM | 1000-1090 | Accepts input of the original matrix. |
| Q | 2100-2120 | Clears screen and exits program. |
In addition, there are four workhorse subroutines that are called by most of the main subroutines listed above. A fraction reducer routine at 1400-1470 reduces all fractions and also serves to find least common denominators for additions. A matrix switcher at 1500-1560 is the entry routine and the *R and *R + routines. The move current to current-1 routine at 1600-1650 is used by the *R, *R + , IR, and B routines.
DATA STRUCTURE
************************************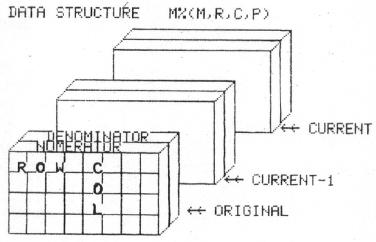
Three matrices are stored as one four-dimensioned array M%(M, R, C, P). M is the matrix number with 1 = original, 2 = current-1, and 3 = current. R is the row number and C is the column number. P = 1 means numerator and P = 2 means denominator. The denominator for any integer has a value of 1. An integer array name (M%) was chosen to conserve memory so that this program can be effective in an 8K machine. This limits any numerator or denominator to the maximum integer size and occasionally causes overflow problems. This occurs in large matrix problems with many relatively prime factors. It happens seldom but a check has been patched in to detect this and give you the chance to back up one step and try something else.
Summary
This program has three notable weaknesses. It has no provisions for work on matrices with decimal entries and it's use in the classroom does require a minimal amount of time and planning for equipment set-up. It also bombs occasionally as mentioned above under data structure. The strengths of this program far outweight the weaknesses and make it an effective teaching tool. It allows concentration on strategy and concepts rather than details. It handles fractions the way the students are expected to, displaying results and accepting input in a human rather than a computer way. It has saved my students and me valuable classtime and has led them to a better understanding of the ideas being taught. In addition, it can be used outside of class for a variety of applications.
I hope other mathematics teachers will find this program as useful as I have. If you don't wish to spend your time keying the program into your machine, I will be happy to send you a copy on tape. Send a check for $10.00 and your name and complete address to William L. Hinrichs, 5056 Welsh Ct., Rockford, 111., 61107.